题目内容
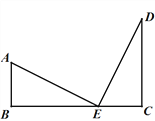
【题目】如图E在BC上,AB⊥BC于B,DC⊥BC于C,连结AE、DE,AE=DE.若AB=20,DC=40,BC=60.
(1)求DE的长
(2)求∠AED的度数
【答案】(1)20![]() (2)∠AED=90°
(2)∠AED=90°
【解析】试题分析:(1)设BE=x,利用勾股定理表示出AE2、DE2,然后根据AE=DE列出方程求出x,再由勾股定理即可得出结论:
(2)再利用“HL”证明Rt△ABE和Rt△EDC全等根据全等三角形对应角相等可得∠AEB=∠D,再根据平角等于180°列式计算即可求出∠AED=90°.
试题解析:解:(1)∵AB⊥BC,CD⊥BC,∴∠ABC=∠DCB=90°,设BE=x,在Rt△ABE和Rt△DCE中,根据勾股定理得,AB2+BE2=AE2,DC2+CE2=DE2,∵AE=DE,∴AB2+BE2=DC2+CE2,∴202+x2=(60-x)2+402,解得x=40,即DE=![]() =
=![]() =
=![]() ;
;
(2)在Rt△ABE和Rt△DCE中,∵AE=DE,BE=CD=40,∴Rt△ABE≌Rt△DCE(HL),∴∠AEB=∠D,∵∠CED+∠D=90°,∴∠CED+∠AEB=90°,∴∠AED=180°﹣∠CED﹣∠AEB=180°﹣90°=90°.

练习册系列答案
相关题目