题目内容
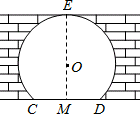 如图是无为中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.
如图是无为中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.
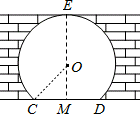 解:连接OC.设⊙O的半径为xm,
解:连接OC.设⊙O的半径为xm,∵EM⊥CD,
∴CM=
 CD=1m.
CD=1m.在Rt△OCM中,由OM2+CM2=OC2,
得(3-x)2+1=x2.
解得:x=
 .
.答:构成该拱门的⊙O的半径为
 m
m分析:连接OC,设半径为xm,由题意可得EF⊥CD,点O在EF上,在Rt△OCM中,利用勾股x定理即可得出的值.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,再利用勾股定理得出结论是解答此题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
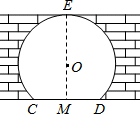 如图是无为中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.
如图是无为中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.