题目内容
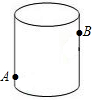 如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.
如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.
请问:蚂蚁爬到食物处的最近路线是多长?
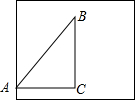 解:将圆柱的侧面展开,小蚂蚁到达目的地的最近距离为线段AB的长.
解:将圆柱的侧面展开,小蚂蚁到达目的地的最近距离为线段AB的长.由勾股定理,AB2=AC2+BC2=122+(18-1-1)2=400,
AB=20 cm.
分析:首先画出圆柱的侧面展开图,进而得到AC=12cm,BC=18-2=16cm,再利用勾股定理计算出AB长即可.
点评:此题主要考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
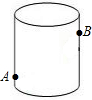 如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.
如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.