题目内容
操作实验:
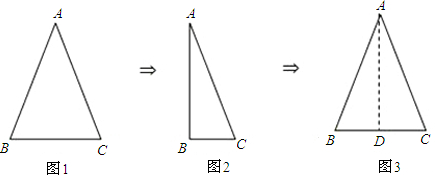
如图,把等腰三角形沿顶角平分线对折并展开,发现被折痕分成的两个三角形成轴对称.
所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等.
根据上述内容,回答下列问题:
思考验证:如图(4),在△ABC中,AB=AC.试说明∠B=∠C的理由;
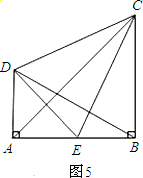
探究应用:如图(5),CB⊥AB,垂足为A,DA⊥AB,垂足为B.E为AB的中点,AB=BC,CE⊥BD.
(1)BE与AD是否相等,为什么?
(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;
(3)∠DBC与∠DCB相等吗试?说明理由.

如图,把等腰三角形沿顶角平分线对折并展开,发现被折痕分成的两个三角形成轴对称.
所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等.
根据上述内容,回答下列问题:
思考验证:如图(4),在△ABC中,AB=AC.试说明∠B=∠C的理由;


探究应用:如图(5),CB⊥AB,垂足为A,DA⊥AB,垂足为B.E为AB的中点,AB=BC,CE⊥BD.
(1)BE与AD是否相等,为什么?
(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;
(3)∠DBC与∠DCB相等吗试?说明理由.
思考验证:
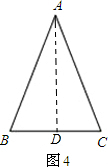
过A点作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
,
∴△ABD≌△ACD(HL),
∴∠B=∠C;
探究应用:
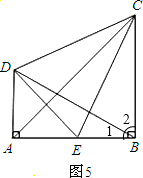
(1)说明:因为CB⊥AB,
∴∠CBA=90°.
∴∠1+∠2=90°.
∵DA⊥AB,
∴∠DAB=90°.
∴∠ADB+∠1=90°.
∴∠ADB=∠2.
在△ADB和△BEC中
,
∴△DAB≌△EBC(ASA).
∴DA=BE.
(2)∵E是AB中点,
∴AE=BE.
∵AD=BE,
∴AE=AD.
在△ABC中,因为AB=BC,
∴∠BAC=∠BCA.
∵AD∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠DAC.
在△ADC和△AEC中,
,
∴△ADC≌△AEC(SAS).
∴DC=CE.
∴C在线段DE的垂直平分线上.
∵AD=AE,
∴A在线段DE的垂直平分线上.
∴AC垂直平分DE.
(3)∵AC是线段DE的垂直平分线,
∴CD=CE.
∵△ADB≌△BEC,
∴DB=CE.
∴CD=BD.
∴∠DBC=∠DCB.

过A点作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
|
∴△ABD≌△ACD(HL),
∴∠B=∠C;
探究应用:

(1)说明:因为CB⊥AB,
∴∠CBA=90°.
∴∠1+∠2=90°.
∵DA⊥AB,
∴∠DAB=90°.
∴∠ADB+∠1=90°.
∴∠ADB=∠2.
在△ADB和△BEC中
|
∴△DAB≌△EBC(ASA).
∴DA=BE.
(2)∵E是AB中点,
∴AE=BE.
∵AD=BE,
∴AE=AD.
在△ABC中,因为AB=BC,
∴∠BAC=∠BCA.
∵AD∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠DAC.
在△ADC和△AEC中,
|
∴△ADC≌△AEC(SAS).
∴DC=CE.
∴C在线段DE的垂直平分线上.
∵AD=AE,
∴A在线段DE的垂直平分线上.
∴AC垂直平分DE.
(3)∵AC是线段DE的垂直平分线,
∴CD=CE.
∵△ADB≌△BEC,
∴DB=CE.
∴CD=BD.
∴∠DBC=∠DCB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 = ;
= ; 
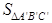 = ;
= ;