题目内容
正方形的对角长为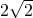 ,那么正方形的对角线的交点到各边的距离为
,那么正方形的对角线的交点到各边的距离为
- A.1
- B.

- C.2
- D.

A
分析:根据正方形对角线互相垂直平分的性质,可以证明△OCD为等腰直角三角形,因为OE⊥CD,所以E为CD的中点,根据斜边中线长为斜边的一半可以求得OE= CD,∵CD=
CD,∵CD= =2,故OE=1.
=2,故OE=1.
解答: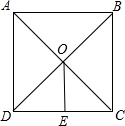 解:图中OE为O到CD边的距离,即OE⊥CD,
解:图中OE为O到CD边的距离,即OE⊥CD,
∵正方形对角线互相垂直平分,
∴OD=OC,OD⊥OC,
即△OCD为等腰直角三角形,
∵OE⊥CD,
∴E为CD的中点,即OE为斜边CD的中线,
∴OE= CD,
CD,
∵在等腰Rt△ADC中,AD=DC,AC=2 ,
,
∴AD= =2,
=2,
即OE=1.
故选A.
点评:本题考查了直角三角形中勾股定理的运用,考查了正方形各边长相等、各内角为直角的性质,考查了正方形对角线互相垂直平分的性质,本题中正确求OE= CD是解题的关键.
CD是解题的关键.
分析:根据正方形对角线互相垂直平分的性质,可以证明△OCD为等腰直角三角形,因为OE⊥CD,所以E为CD的中点,根据斜边中线长为斜边的一半可以求得OE=
 CD,∵CD=
CD,∵CD= =2,故OE=1.
=2,故OE=1.解答:
 解:图中OE为O到CD边的距离,即OE⊥CD,
解:图中OE为O到CD边的距离,即OE⊥CD,∵正方形对角线互相垂直平分,
∴OD=OC,OD⊥OC,
即△OCD为等腰直角三角形,
∵OE⊥CD,
∴E为CD的中点,即OE为斜边CD的中线,
∴OE=
 CD,
CD,∵在等腰Rt△ADC中,AD=DC,AC=2
 ,
,∴AD=
 =2,
=2,即OE=1.
故选A.
点评:本题考查了直角三角形中勾股定理的运用,考查了正方形各边长相等、各内角为直角的性质,考查了正方形对角线互相垂直平分的性质,本题中正确求OE=
 CD是解题的关键.
CD是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,AD=4,BC=8,则AE的长为
如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,AD=4,BC=8,则AE的长为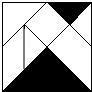 七巧板中(如图所示)小阴影部分的面积是大阴影部分面积的
七巧板中(如图所示)小阴影部分的面积是大阴影部分面积的


 如图,已知点A是以MN为直径的半圆上一个三等分点,点B是
如图,已知点A是以MN为直径的半圆上一个三等分点,点B是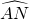 的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为
的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为
 已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD
已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD