Question

【题目】如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC，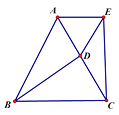

（1）说明△BCD与△CAE全等的理由
（2）请判断△ADE的形状，并说明理由．

Answer 1

【答案】
（1）解：∵△ABC是等边三角形

∴AB=BC=AC，∠ACB=60°

又∵D为AC中点

∴BD⊥AC，AD=CD

又∵AE⊥EC

∴∠BDC=∠AEC=90°

又∵BD=CE

∴Rt△BDC≌Rt△CEA

（2）解：∵Rt△BDC≌Rt△CEA

∴∠EAC=∠ACB=60°，AE=CD

又∵D为边AC的中点，

∴AD=CD，

∴AD=AE

∴△ADE是等边三角形．

【解析】（1）利用等边三角形的性质和“HL"可判定全等；（2）由（1）的结论和已知，利用”有一个角为60度的等腰三角形是等边三角形“证出结论.