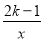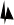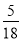题目内容
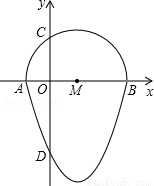
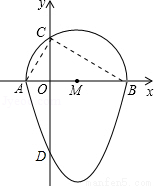
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为
3+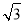 .
.
【解析】
试题分析:连接AC,BC,有抛物线的解析式可求出A,B,C的坐标,进而求出AO,BO,DO的长,在直角三角形ACB中,利用射影定理可求出CO的长,进而可求出CD的长.
试题解析:连接AC,BC,
∵抛物线的解析式为y=x2-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3,
设y=0,则0=x2-2x-3,
解得:x=-1或3,
∴A(-1,0),B(3,0)
∴AO=1,BO=3,
∵AB为半圆的直径,
∴∠ACB=90°,
∵CO⊥AB,
∴CO2=AO•BO=3,
∴CO=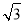 ,
,
∴CD=CO+OD=3+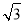 .
.
考点:二次函数综合题.

练习册系列答案
相关题目
汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了“献出我们的爱”赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?