题目内容
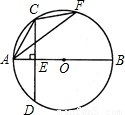
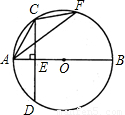
如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.(1)求证:∠ACE=∠AFC;
(2)若CD=BE=8,求sin∠AFC的值.
【答案】分析:(1)由垂径定理得出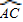 =
= ,再由圆周角定理即可得出∠ACE=∠AFC;
,再由圆周角定理即可得出∠ACE=∠AFC;
(2)连接OC,设圆的半径为r,在直角三角形OCE中,由勾股定理得出r,由于∠ACE=∠AFC;可在直角三角形ACE中求得答案.
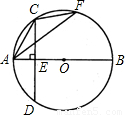
解答: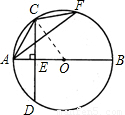 (1)证明:∵AB是⊙O的直径,CD⊥AB,
(1)证明:∵AB是⊙O的直径,CD⊥AB,
∴AC=AD,
∴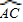 =
=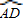 ,
,
∴∠ACE=∠AFC;
(2)解:连接OC,
设圆的半径为r,
∵CD=BE=8,
∴CE=4,OE=8-r,
∴在直角三角形OCE中,
r2-(8-r)2=16,
∴r=5,
∴AE=2,
∴AC=2 ,
,
∴sin∠AFC=sin∠ACE= =
=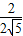 =
= .
.
点评:本题考查了垂径定理、圆周角定理、勾股定理以及锐角三角函数的定义,是基础知识要熟练掌握.
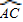 =
= ,再由圆周角定理即可得出∠ACE=∠AFC;
,再由圆周角定理即可得出∠ACE=∠AFC;(2)连接OC,设圆的半径为r,在直角三角形OCE中,由勾股定理得出r,由于∠ACE=∠AFC;可在直角三角形ACE中求得答案.
解答:
 (1)证明:∵AB是⊙O的直径,CD⊥AB,
(1)证明:∵AB是⊙O的直径,CD⊥AB,∴AC=AD,
∴
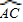 =
=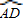 ,
,∴∠ACE=∠AFC;
(2)解:连接OC,
设圆的半径为r,
∵CD=BE=8,
∴CE=4,OE=8-r,
∴在直角三角形OCE中,
r2-(8-r)2=16,
∴r=5,
∴AE=2,
∴AC=2
 ,
,∴sin∠AFC=sin∠ACE=
 =
=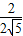 =
= .
.点评:本题考查了垂径定理、圆周角定理、勾股定理以及锐角三角函数的定义,是基础知识要熟练掌握.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
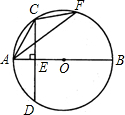 如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.
如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.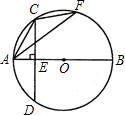 如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.
如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.