题目内容
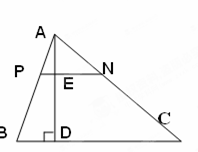
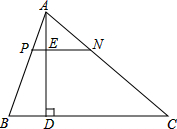已知如图，PN∥BC，AD⊥BC交PN于E，交BC于D（1）若AP：PB=1：2，S△ABC=18cm2，求S△APN；
（2）若
| S△APN |
| S四边形PBCN |
| 1 |
| 3 |
| AE |
| AD |
分析：（1）由PN∥BC，可得△APN∽△ABC，又由AP：PB=1：2，S△ABC=18cm2，然后由相似三角形面积比等于相似比的平方，求得S△APN；
（2）由PN∥BC，AD⊥BC，
=
，根据相似三角形的面积比等于相似比的平方，即可求得答案．
（2）由PN∥BC，AD⊥BC，
| S△APN |
| S四边形PBCN |
| 1 |
| 3 |
解答：解：（1）∵AP：PB=1：2，
∴AP：AB=1：3，
∵PN∥BC，
∴△APN∽△ABC，
∴
=（
）2=
，
∵S△ABC=18cm2，
∴S△APN=2cm2；
（2）∵PN∥BC，AD⊥BC，
∴AE⊥PN，
∵
=
，
∴
=
，
∵△APN∽△ABC，
∴
=（
）2=
，
∴
=
．
∴AP：AB=1：3，
∵PN∥BC，
∴△APN∽△ABC，
∴
| S△APN |
| S△ABC |
| AP |
| AB |
| 1 |
| 9 |
∵S△ABC=18cm2，
∴S△APN=2cm2；
（2）∵PN∥BC，AD⊥BC，
∴AE⊥PN，
∵
| S△APN |
| S四边形PBCN |
| 1 |
| 3 |
∴
| S△APN |
| S△ABC |
| 1 |
| 4 |
∵△APN∽△ABC，
∴
| S△APN |
| S△ABC |
| AE |
| AD |
| 1 |
| 4 |
∴
| AE |
| AD |
| 1 |
| 2 |
点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
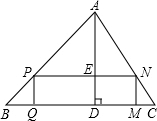已知如图，△ABC中BC=60cm，高AD=40cm，四边形PQMN是矩形，点P在AB边上，点Q、M在BC边上，点N在AC边上．
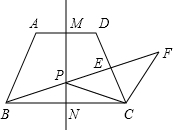的对称轴，点P是线段MN上一个动点（不与M、N重合），射线BP交线段CD于点E，过点C作CF∥AB交射线BP于点F．
已知如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：
，求
；
，求
的值.