Question

两座灯塔A和B与海岸观察站S的距离相等，A在S北偏东30°方向，B在S的南偏东60°方向，则灯塔B在灯塔A的________方向．

Answer 1

南偏东15°
分析：首先根据题意画出图形，然后由方向角及平角的定义求出∠ASB的度数，再根据等腰三角形及三角形内角和定理得出∠SAB=45°，由平行线性质得出∠SAD=30°，从而得出∠BAD的度数．
解答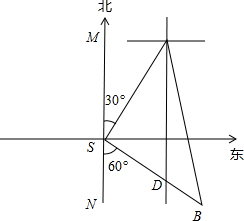：解：由题意得∠MSA=30°，∠NSB=60°，
∴∠ASB=180°-30°-60°=90°，
∵AS=BS，
∴∠SAB=45°．
∵MN∥AD，
∴∠SAD=∠MSA=30°，
∴∠BAD=∠SAB-∠SAD=45°-30°=15°．
∴灯塔B在灯塔A的南偏东15°．
故答案为：南偏东15°．
点评：本题考查了方向角、平角的定义，等腰三角形的性质，三角形内角和定理及平行线的性质，综合性较强，难度中等．