题目内容
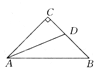
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.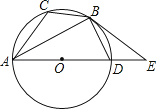
(1)求证:BE是⊙O的切线;
(2)若BC= ![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
【答案】
(1)
证明:如图,
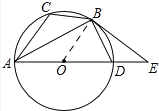
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线,
(2)
解:如图2,
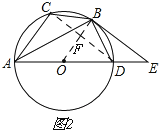
设圆的半径为R,连接CD,
∵AD为⊙O的直径,
∴∠ACCD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF= ![]() AC=
AC= ![]() ,
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴ ![]() ,
,
∴ ![]() ,
,
∴DE= ![]() ,
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴ ![]() ,
,
∴ 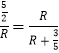 ,
,
∵R>0,
∴R=3,
∵BE是⊙O的切线,
∴BE= ![]() =
= ![]() =
= ![]()
【解析】(1)先根据等弦所对的劣弧相等,再结合∠EBD=∠CAB从而得到∠BAD=∠EBD,最后用直径所对的圆周角为直角即可;(2)利用三角形的中位线先求出OF,再用平行线分线段成比例定理求出半径R,最后用切割线定理即可.此题是切线的判定,主要考查了圆周角的性质,切线的判定,平行线分线段成比例定理,相似三角形的判定和相似,圆内接四边形的性质,解本题的关键是作出辅助线.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目