Question

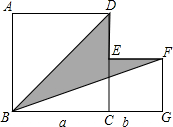
如图，已知等腰直角△ACB的边AC=BC=a，等腰直角△BED的边BE=DE=b，且a＜b，点C、B、E在一条直线上，连接AD．
（1）求△ABD的面积；
（2）如果点P是线段CE的中点，连接AP、DP得到△APD，求△APD的面积．
（以上结果先用含a、b代数式表示，后化简）

Answer 1

（1）∵AC=BC=a，BE=DE=b，
∴S_△ABD=S_梯形ACED-S_△ABC-S_△BDE
=

1

2

（a+b）（a+b）-

1

2

a²-

1

2

b²
=

1

2

（a²+2ab+b²-a²-b²）
=ab；

（2）∵P为CE的中点，
∴CP=EP=

1

2

（a+b），
∴S_△APD=S_梯形ACED-S_△APC-S_△BEP
=

1

2

（a+b）（a+b）-

1

2

a•

a+b

2

-

1

2

b•

a+b

2

=

1

2

a²+ab+

1

2

b²-

1

4

a²-

1

4

ab-

1

4

ab-

1

4

b²
=

1

4

（a+b）²．