��Ŀ����
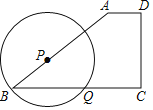
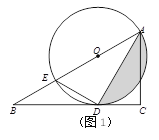
����Ŀ����ͼ����Rt��ABC�У���C��90����OΪб��AB��һ�㣬��OΪԲ�ġ�OAΪ�뾶��Բǡ����BC�����ڵ�D����AB����һ������ΪE������DE��
��1�����ҳ�ͼ������ADE���Ƶ������Σ���˵�����ɣ�
��2����AC��3��AE��4������ͼ����Ӱ���ֵ������
��3��С���ڽ��������˼������һ�����⣺��ͼ�еġ�O��Բ�ľ�������ôȷ�����أ���������ͼ������ֱ�ߺ�Բ���ҵ����������Բ��O����д�������ͼ������
���𰸡�(1)������;(2)![]() �У�
��![]() ;(3)������.
;(3)������.
��������
��1��BCΪԲO�����ߣ�����OD�����Ƴ���EAD=��ODA=��DAC���ɡ�EDA=��DCA=90�������Ƴ���AED�ס�ADC��
��2��������AED�ס�ADC���ɵó�AD�ij��ȣ��ٸ�����AED�����߱�����ϵ�����Ƴ���AOD=120����������������������ε�������ɵõ���Ӱ���������
��3��������BAC�Ľ�ƽ���߽�BC���ڵ�D���ڹ���D��BC�Ĵ��߽�AB�ڵ�O����ע��������Ψһ��
�⣺��1����ACD����ADE���ƣ���ͼ��1����ʾ��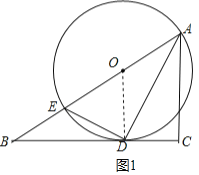
����OD���ߡ�Oǡ����BC�����ڵ�D��
���ODB=90����
�֡ߡ�C=90����
��OD��AC��
���ODA=��DAC��
��OD=OA��
���ODA=��OAD��
���OAD=��DAC��
��AEΪ��O��ֱ����
���ADE=90����
���ADE=��C��
���ACD�ס�ADE��
��2���ߡ�ACD�ס�ADE��
��![]() ��
��
��AD=2![]() ��
��
��AC=3�����ݹ��ɶ�����CD=![]() ��
��
��sin��DAC=![]() ��
��
���DAC=��EAD=��ODA=30����
���AOD=120����
��S��OAD=![]() OA2=
OA2=![]() ��
��
��S=![]() ��
��
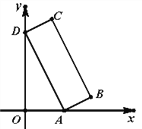
��3����ͼ2��ʾ����ͼ������
����AΪԲ�ģ�AC��Ϊ�뾶��������AB�ڵ�H����H��CΪԲ�ģ�����![]() CH��Ϊ�뾶���������ڵ�G������AG��AG��Ϊ��BAC�Ľ�ƽ���ߣ�AG��BC�Ľ��㼴Ϊ��D��
CH��Ϊ�뾶���������ڵ�G������AG��AG��Ϊ��BAC�Ľ�ƽ���ߣ�AG��BC�Ľ��㼴Ϊ��D��
����DΪԲ�ģ�DC��Ϊ�뾶��������BD�ڵ�C������C��C��ΪԲ�ģ�����![]() CC��Ϊ�뾶�������ֱ��ڵ�E��F������EF��EF��ΪCC���Ĵ�ֱƽ���ߣ�EF��AB�Ľ��㼴Ϊ��O��
CC��Ϊ�뾶�������ֱ��ڵ�E��F������EF��EF��ΪCC���Ĵ�ֱƽ���ߣ�EF��AB�Ľ��㼴Ϊ��O��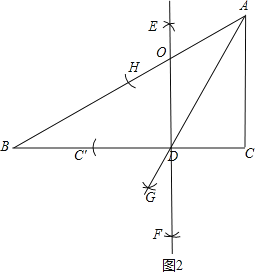

 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�