题目内容
【题目】如图，在平行四边形ABCD中，AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线，AQ与BN相交于点P，CN与DQ相交于点M，判断四边形MNPQ的形状，并证明你的结论．
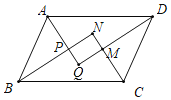
【答案】四边形MNPQ是矩形，理由见解析.
【解析】
可得出一个结论，即“四边形PQMN为矩形”．因为平行四边形中邻角互补，所以其每两个相邻内角的平分线都互相垂直，从而根据有三个角是直角的四边形是矩形来判定．
四边形MNPQ是矩形，理由如下：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAB+∠ABC＝180°,
∵AP，BN分别平分∠DAB，∠ABC，
∴∠PAB+∠PBA＝
(∠DAB+∠ABC)＝×180°＝90°,
∴∠NPQ＝∠APB＝90°，
同理：∠N＝90°，∠AQD＝90°，
∴四边形MNPQ是矩形．
练习册系列答案
相关题目
【题目】（本题有两道题，请从（1）、（2）题中选一题作答即可）
（1）某品牌太阳镜由一个镜架和两个镜片配套构成，每个工人每天可以加工
个镜架或者加工
个镜片，现有
名工人，应怎么安排人力，才能使每天生产的镜架和镜片配套？能做成多少副太阳镜？
（2）去年春季，蔬菜种植场在
公顷的大棚地里分别种植了茄子和西红柿，总费用是
万元.其中，种植茄子和西红柿每公顷的费用和每公顷获利情况如表：
每公顷费用 万元 | 每公顷获利 万元 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题：
①求出茄子和西红柿的种植面积各为多少公顷？
②种植场在这一季共获利多少万元？
