Question

（2012•佳木斯）如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（1）将△ABC向右平移3个单位长度再向下平移2个单位长度，画出两次平移后的△A₁B₁C₁；
（2）写出A₁、C₁的坐标；
（3）将△A₁B₁C₁绕C₁逆时针旋转90°，画出旋转后的△A₂B₂C₁，求线段B₁C₁旋转过程中扫过的面积（结果保留π）．

Answer 1

分析：（1）根据图形平移的性质画出两次平移后的△A₁B₁C₁即可；
（2）根据△A₁B₁C₁在坐标系中的位置写出A₁、C₁的坐标；
（3）根据图形旋转的性质画出旋转后的△A₂B₂C₁，再根据勾股定理求出B₁C₁的长，由扇形的面积公式即可计算出线段B₁C₁旋转过程中扫过的面积．

解答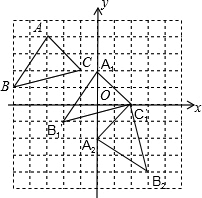：解：（1）如图所示：

（2）由△A₁B₁C₁在坐标系中的位置可知，A₁（0，2）；C₁（2，0）；

（3）旋转后的图形如图所示：
∵由勾股定理可知，B₁C₁=

12+42

=

17

，
∴S_扇形=

90π×( 17 )2

360

=

17

4

π．

点评：本题考查的是图形的旋转、平移及扇形面积的计算，熟知图形旋转、平移后的图形与原图形全等是解答此题的关键．