Question

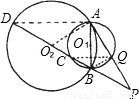
（2001•山东）如图，⊙O₂过⊙O₁直径AB的两端，DB为⊙O₂的直径，交⊙O₁于C点．点Q在⊙O₁上，连接AQ并延长交DB的延长线于点P，且PA•PC=PQ•PD．
（1）求证：PA是⊙O₂的切线；
（2）若AQ=6cm，∠P=30°，求PB的长．

Answer 1

【答案】分析：（1）要证PA是⊙O的切线，只要证明其符合切线定理即可；
（2）通过∠P的余弦得出PB的长．
解答：（1）证明：连接AD，AO₂，CQ，BQ；
∵在⊙O₁中，PQ•PA=PB•PC，
∵PA•PC=PQ•PD，
∴PA•PA=PB•PD，
∴PA是⊙O₂的切线；

（2）解：∵BAP=∠D=∠P=30°，AQ=PQ，
∴BP=6÷cos30°=4．
点评：本题考查了切线的判定．要证某线是圆的切线，连接圆心与这点（即为半径），根据切线的性质得出．同时考查了三角函数的运用．