题目内容
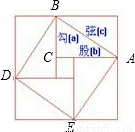
给出下列命题:①反比例函数 的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )
的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )
A.③④
B.①②③
C.②④
D.①②③④
【答案】分析:分别根据反比例函数的性质、矩形的性质及勾股定理、圆心角、弧、弦的关系对每小题进行逐一解答.
解答:解:①反比例函数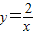 的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;
的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;
②对角线相等且有一个内角是直角的四边形有可能是梯形,故此小题错误;
③符合勾股定理的历史,故此小题正确;
④符合圆心角、弧、弦的关系,故此小题正确.
所以③④正确.
故选A.
点评:本题考查的是反比例函数的性质、矩形的性质及勾股定理、圆心角、弧、弦的关系,是一道较为简单的题目.
解答:解:①反比例函数
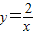 的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;
的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;②对角线相等且有一个内角是直角的四边形有可能是梯形,故此小题错误;
③符合勾股定理的历史,故此小题正确;
④符合圆心角、弧、弦的关系,故此小题正确.
所以③④正确.
故选A.
点评:本题考查的是反比例函数的性质、矩形的性质及勾股定理、圆心角、弧、弦的关系,是一道较为简单的题目.

练习册系列答案
相关题目
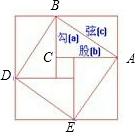 给出下列命题:①反比例函数
给出下列命题:①反比例函数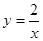 的图象经过一、三象限,且
的图象经过一、三象限,且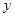 随
随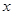 的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是(
▲ )
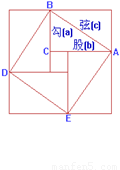
的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是(
▲ )
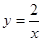 的图象经过一、三象限,且
的图象经过一、三象限,且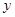 随
随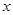 的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是( )
的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是( )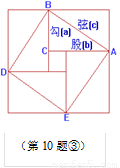
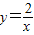 的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )
的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )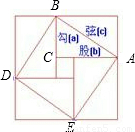
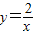 的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )
的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )