题目内容
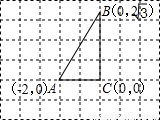
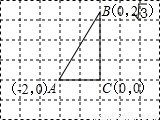
如图是一张传说中的“藏宝图”,图上除标明了A﹑B﹑C三点的位置以外,并没有直接标出”宝藏”的位置,但图上注有寻找“宝藏”的方法:把直角△ABC补成矩形,使矩形的面积是A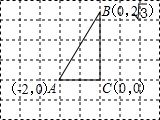 BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是
BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是分析:如何补成符合要求的矩形是关键.有2种方法:①以两直角边为邻边组成矩形;②以斜边为一边,直角顶点在对边上补成矩形.分别根据图形计算求解.
解答:解:由图上可知,以原三角形的直角顶点为坐标原点建立平面直角坐标系,直角三角形的两个锐角分别为30°和60°,两条直角边长分别为2和2
,且把直角△ABC补成矩形,有三种可能:
(1)让相同的直角三角形与原三角形斜边重合的,这样面积为原来的2倍,另一个顶点坐标为(2,2
);
(2)以原三角形的斜边为矩形的一边补成矩形,如图所示:
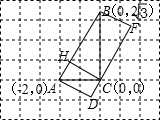
在原三角形的斜边上作出过直角顶点的高,垂足为点H,则把原三角形分成两个直角三角形了,以长为2的直角边为斜边,再补一个与这个小直角三角形重合斜边的小直角三角形的顶点D,即为矩形的顶点D,以长为2
的直角边为斜边,再补一个与这个小直角三角形重合斜边的小直角三角形的顶点F,即为矩形的顶点F,
则点D到坐标原点的距离=2×cos60°=2×
=1,D点的横坐标=-1×cos60°=-
,点D的纵坐标=-1×sin60°=-
,点D的坐标为(-
,-
);
点F到原点的距离=2
×cos30°=3,F点的横坐标=3×cos60°=
,
点F的纵坐标=3×sin60°=-
,点F的坐标为(
,
).
所以填:(2,2
)或(-
,-
)或(
,
).
| 3 |
(1)让相同的直角三角形与原三角形斜边重合的,这样面积为原来的2倍,另一个顶点坐标为(2,2
| 3 |
(2)以原三角形的斜边为矩形的一边补成矩形,如图所示:

在原三角形的斜边上作出过直角顶点的高,垂足为点H,则把原三角形分成两个直角三角形了,以长为2的直角边为斜边,再补一个与这个小直角三角形重合斜边的小直角三角形的顶点D,即为矩形的顶点D,以长为2
| 3 |
则点D到坐标原点的距离=2×cos60°=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点F到原点的距离=2
| 3 |
| 3 |
| 2 |
点F的纵坐标=3×sin60°=-
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
所以填:(2,2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
点评:本题考查了在平面直角坐标系中用特殊三角函数求点坐标的能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是________.(用坐标表示)
BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是________.(用坐标表示)