题目内容
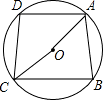 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于
如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于
- A.20°
- B.30°
- C.40°
- D.50°
B
分析:连接OD,根据已知及全等三角形的判定得到△ADO≌△CDO,从而得到对应角相等,再根据圆周角定理及平行线的性质即可求得∠BCO的度数.
解答: 解:连接OD,
解:连接OD,
∵AO=OC=OD,DA=DC,
∴△ADO≌△CDO.
∴∠COD=∠AOD= ∠AOC=80°.
∠AOC=80°.
∴∠ODC=∠OCD=∠ODA=∠OAD=50°.
∴∠CDA=100°.
∵AD∥BC,
∴∠DCB=180°-∠CDA=180°-100°=80°.
∴∠BCO=∠BCD-∠OCD=80°-50°=30°.
故选B.
点评:解答此题的关键是作出辅助线,构造出全等三角形,利用全等三角形及等腰三角形的性质结合圆心角与圆周角的关系解答.
分析:连接OD,根据已知及全等三角形的判定得到△ADO≌△CDO,从而得到对应角相等,再根据圆周角定理及平行线的性质即可求得∠BCO的度数.
解答:
 解:连接OD,
解:连接OD,∵AO=OC=OD,DA=DC,
∴△ADO≌△CDO.
∴∠COD=∠AOD=
 ∠AOC=80°.
∠AOC=80°.∴∠ODC=∠OCD=∠ODA=∠OAD=50°.
∴∠CDA=100°.
∵AD∥BC,
∴∠DCB=180°-∠CDA=180°-100°=80°.
∴∠BCO=∠BCD-∠OCD=80°-50°=30°.
故选B.
点评:解答此题的关键是作出辅助线,构造出全等三角形,利用全等三角形及等腰三角形的性质结合圆心角与圆周角的关系解答.

练习册系列答案
相关题目
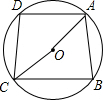 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )
如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )| A、20° | B、30° | C、40° | D、50° |
下列结论不正确的是( )
A、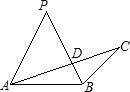 如图,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于6 | B、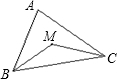 M是△ABC的内心,∠BMC=130°,则∠A的度数为50° | C、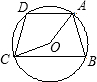 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于80° | D、若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是120° |
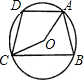 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于
如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于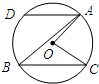 如图,⊙O中,弦AD平行于弦BC,∠AOC=78°,求∠DAB的度数.
如图,⊙O中,弦AD平行于弦BC,∠AOC=78°,求∠DAB的度数.