题目内容
 如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).
如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).(1)当x=
5
5
时,S△PAB=5平方米.(本题不要求写过程)(2)当x为何值时,BP的距离为6米?
(3)当x为何值时,△PAB的周长为10米?
分析:(1)根据题意可得AP=x,则可表示出△ABP的面积,令面积等于5,即可得出x的值;
(2)AP=x,利用勾股定理,表示出BP,建立方程,解出x的值即可;
(3)分别表示出AP、BP,然后根据△PAB的周长为10米,可建立方程,解出即可.
(2)AP=x,利用勾股定理,表示出BP,建立方程,解出x的值即可;
(3)分别表示出AP、BP,然后根据△PAB的周长为10米,可建立方程,解出即可.
解答:解:(1)由题意得,AP=x,S△ABP=
AP×AB=x,
故当x=5时,S△PAB=5平方米;
(2)AP=x,
由题意得,AP2+AB2=BP2,即x2+22=62,
解得:x=4
,即当x=4
时,BP的距离为6米.
(3)AP=x,BP=
,
由题意得:x+
+2=10,
解得:x=
,即当x等于
时,△PAB的周长为10米.
| 1 |
| 2 |
故当x=5时,S△PAB=5平方米;
(2)AP=x,
由题意得,AP2+AB2=BP2,即x2+22=62,
解得:x=4
| 2 |
| 2 |
(3)AP=x,BP=
| x2+22 |
由题意得:x+
| x2+22 |
解得:x=
| 15 |
| 4 |
| 15 |
| 4 |
点评:此题考查了勾股定理的知识,解答本题的关键是正确的表示出AP、BP的长度,注意掌握勾股定理的形式.

练习册系列答案
相关题目
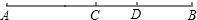 如图,线段AB长为16cm,C是AB的中点,D是BC的中点,则线段DC的长为
如图,线段AB长为16cm,C是AB的中点,D是BC的中点,则线段DC的长为
 如图,线段AB长为16cm,C是AB的中点,D是BC的中点,则线段DC的长为________cm.
如图,线段AB长为16cm,C是AB的中点,D是BC的中点,则线段DC的长为________cm.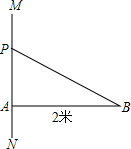 如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).
如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).