题目内容
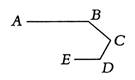
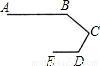
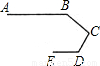
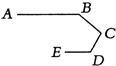5、如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为（ ）分析：先作辅助线CF∥AB，再根据平行线的性质解答即可．
解答：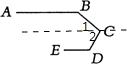
解：过点C作CF∥AB，
∵AB∥DE，
∴AB∥DE∥CF，
∴∠B+∠1=180°，∠D+∠2=180°；
故∠B+∠1+∠D+∠2=360°，即∠B+∠BCD+∠D=360°，
故∠BCD=360°-140°-120°=100°．
故选B．
解：过点C作CF∥AB，
∵AB∥DE，
∴AB∥DE∥CF，
∴∠B+∠1=180°，∠D+∠2=180°；
故∠B+∠1+∠D+∠2=360°，即∠B+∠BCD+∠D=360°，
故∠BCD=360°-140°-120°=100°．
故选B．
点评：注意此类题要作出辅助线，运用平行线的性质探求三个角的关系．
练习册系列答案
相关题目
17、如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为
