题目内容
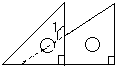
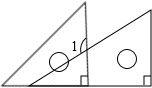
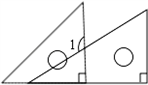
如图，将一副三角板如图所示叠放在一起，若AB=8cm，则阴影部分的面积是________cm2．
8
分析：由于BC∥DE，那么△ACF也是等腰直角三角形，欲求其面积，必须先求出直角边AC的长；Rt△ABC中，已知斜边AB及∠B的度数，易求得AC的长，进而可根据三角形面积的计算方法求出阴影部分的面积．
解答：∵∠B=30°，∠ACB=90°，AB=8cm，
∴AC=4cm．
由题意可知BC∥ED，
∴∠AFC=∠ADE=45°，
∴AC=CF=4cm．
故S△ACF=
×4×4=8（cm2）．
故答案为8．
点评：本题考查了相似三角形的判定和性质以及解直角三角形，发现△ACF是等腰直角三角形，并能根据直角三角形的性质求出直角边AC的长，是解答此题的关键．
分析：由于BC∥DE，那么△ACF也是等腰直角三角形，欲求其面积，必须先求出直角边AC的长；Rt△ABC中，已知斜边AB及∠B的度数，易求得AC的长，进而可根据三角形面积的计算方法求出阴影部分的面积．
解答：∵∠B=30°，∠ACB=90°，AB=8cm，
∴AC=4cm．
由题意可知BC∥ED，
∴∠AFC=∠ADE=45°，
∴AC=CF=4cm．
故S△ACF=
×4×4=8（cm2）．故答案为8．
点评：本题考查了相似三角形的判定和性质以及解直角三角形，发现△ACF是等腰直角三角形，并能根据直角三角形的性质求出直角边AC的长，是解答此题的关键．
练习册系列答案
口算能手系列答案
相关题目
