题目内容
【题目】如图,在ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.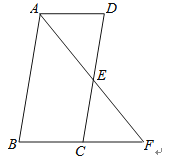
(1)求证:△ADE和△CEF的面积相等
(2)若AB=2AD,试说明AF恰好是∠BAD的平分线
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠F,
∵点E是DC的中点,
∴CE=DE,
在△AED和△FEC
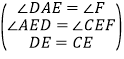 ,
,
∴△AED≌△FEC(AAS),
∴△ADE和△CEF的面积相等
(2)
证明∵四边形ABCD是平行四边形,
∴AD=BC,
∵△AED≌△FEC,
∴AD=CF,
∴AD=BC=CF,
∵AB=2AD,
∴AB=2BC=BF,
∴∠BAF=∠F,
又∵∠DAE=∠F,
∴∠BAF=∠DAE,
即AF是∠BAD的平分线.
【解析】(1)首先根据平行四边形的性质可得AD∥BC,根据平行线的性质可得∠DAE=∠F,然后再证明△AED≌△FEC可得结论;
(2)首先根据平行四边形的性质可得AD=BC,根据全等三角形的性质可得AD=CF,然后再证明AB=BF,进而可得∠BAF=∠F,再由∠DAE=∠F,可得∠BAF=∠DAE,进而可得AF恰好是∠BAD的平分线.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】在小方格纸上按下面的方式涂色:

① ② ③ ④
(1)填表:
图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
涂色的小方格数 |
(2)像这样,第 n 个图形要涂色的小方格数是__________,第100个图形要涂色的小方格数是____________