题目内容
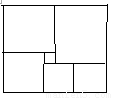
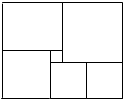 8、如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为1,那么这个矩形色块图的面积为( )
8、如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为1,那么这个矩形色块图的面积为( )分析:设第二个小正方形的边长是x,则其余正方形的边长为:x+1,x+1,x+2,x+3,根据矩形的对边相等得到方程x+x+(x+1)=x+2+x+3,求出x的值,再根据面积公式即可求出答案.
解答:解:设第二个小正方形的边长是x,则其余正方形的边长为:x+1,x+1,x+2,x+3,
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,x+2=6,x+3=7,
∴这个矩形色块图的面积为:1+4×4+4×4+5×5+6×6+7×7=143,
故选B.
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,x+2=6,x+3=7,
∴这个矩形色块图的面积为:1+4×4+4×4+5×5+6×6+7×7=143,
故选B.
点评:本题主要考查了矩形的性质,正方形的性质和面积公式等知识点,解此题的关键是正确设未知数并列出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
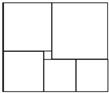 29、如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
29、如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.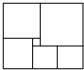 23、如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,则这个矩形色块图的面积为
23、如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,则这个矩形色块图的面积为