题目内容
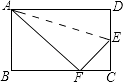
【题目】如图,AD平分∠BAC,AD=AB,CM⊥AD于点M.请你通过观察和测量,猜想线段AB,AC之和与线段AM有怎样的数量关系,并证明你的结论.

【答案】猜想:AB+AC=2AM.证明见解析.
【解析】
根据题目提供的条件和图形中线段的关系,做出猜想AB+AC=2AM,过点C作CE∥AB,CE与AM的延长线交于点E,进一步证明AB+AC=AB+CE=AD+ED=AE,从而得到AB+AC=2AM.
解:猜想:AB+AC=2AM.
证明:过点C作CE∥AB,CE与AM的延长线交于点E.
∴∠ECD=∠B,∠E=∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,∴∠E=∠CAD,∴AC=EC.
又∵CM⊥AD于点M,
∴AM=ME,即AE=2AM.
∵AD=AB,∴∠B=∠ADB.
又∵∠EDC=∠ADB,∴∠ECD=∠EDC,
∴ED=EC,
∴AB+AC=AB+CE=AD+ED=AE,
∴AB+AC=2AM.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/ | -20 | -10 | 0 | 10 | 20 | 30 |
声速/( | 318 | 324 | 330 | 336 | 342 | 348 |
下列说法中错误的是( )
A.在这个变化过程中,当温度为10![]() 时,声速是336
时,声速是336![]()
B.温度越高,声速越快
C.当空气温度为20![]() 时,声音5
时,声音5![]() 可以传播1740
可以传播1740![]()
D.当温度每升高10![]() ,声速增加6
,声速增加6![]()