题目内容
（2012•东营）某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是
30
30
cm．分析：当圆柱形饮水桶的底面半径最大时，圆外接于△ABC；连接外心与B点，可通过勾股定理即可求出圆的半径．
解答：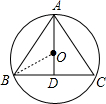
解：连接OB，如图，
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大．
∵AD垂直平分BC，AD=BC=48cm，
∴O点在AD上，BD=24cm；
在Rt△0BD中，设半径为r，则OB=r，OD=48-r，
∴r2=（48-r）2+242，解得r=30．
即圆柱形饮水桶的底面半径的最大值为30cm．
故答案为：30．
解：连接OB，如图，当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大．
∵AD垂直平分BC，AD=BC=48cm，
∴O点在AD上，BD=24cm；
在Rt△0BD中，设半径为r，则OB=r，OD=48-r，
∴r2=（48-r）2+242，解得r=30．
即圆柱形饮水桶的底面半径的最大值为30cm．
故答案为：30．
点评：此题考查把实物图转化为几何图形的能力以及勾股定理，垂径定理的讨论和勾股定理．
练习册系列答案
相关题目
B两组捐款人数的比为1：5．
（2012•东营）如图某天上午9时，向阳号轮船位于A处，观测到某港口城市P位于轮船的北偏西67.5°，轮船以21海里/时的速度向正北方向行驶，下午2时该船到达B处，这时观