题目内容
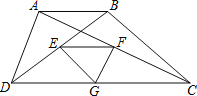
【题目】如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是 .
【答案】9.
【解析】
试题延长EF交BC于点H,可知EF,FH,FG、EG分别为△BDC、△ABC、△BDC和△ACD的中位线,由三角形中位线定理结合条件可求得EF+FG+EG,可求得答案.
解:连接AE,并延长交CD于K,
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
在△AEB和△KED中,
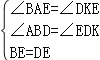 ,
,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=![]() CK=
CK=![]() (DC﹣DK)=
(DC﹣DK)=![]() (DC﹣AB),
(DC﹣AB),
∵EG为△BCD的中位线,∴EG=![]() BC,
BC,
又FG为△ACD的中位线,∴FG=![]() AD,
AD,
∴EG+GF=![]() (AD+BC),
(AD+BC),
∵两腰和是12,即AD+BC=12,两底差是6,即DC﹣AB=6,
∴EG+GF=6,FE=3,
∴△EFG的周长是6+3=9.
故答案为:9.


练习册系列答案
相关题目
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表). 设一个月内使用移动电话主叫的时间为t分钟
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 58元 | 150分钟 | 0.25元/分 | 免费 |
方式二 | 88元 | 350分钟 | 0.19元/分 | 免费 |

(t为正整数),请根据表中提供的信息回答下列问题:
(1)方式一中,当t超过150分钟时,该月费用表示为: 元(用含t的代数式表示);方式二中,当t超过350分钟时,该月费用表示为: 元(用含t的代数式表示).
(2)当t=300时,哪种计费方式的费用较省?请作出判断,并说明理由.