题目内容
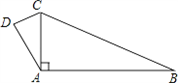
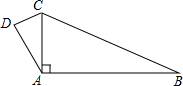 如图,CA⊥AB,AB=8,BC=10,DC=2,AD=
如图,CA⊥AB,AB=8,BC=10,DC=2,AD= ,求四边形ABCD的面积.
,求四边形ABCD的面积.
解:∵CA⊥AB,
∴∠CAB=90°,
∴AC=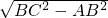 =
=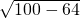 =6,
=6,
∴S△BAC= AB•AC=24;
AB•AC=24;
∵CD2+AD2=AC2,
∴△ACD为直角三角形,
∴S△ADC= AD•DC=
AD•DC= ;
;
∴四边形ABCD的面积为
∴S△BAC+S△ADC=24+ .
.
答:四边形ABCD的面积为24+ .
.
分析:由CA⊥AB,可知∠CAB=90°,在Rt△ABC中运用勾股定理可以求AC的长度,因为AD2+DC2=AC2,所以△ACD为直角三角形,所以四边形ABCD的面积为Rt△ADC和Rt△BAC面积之和.
点评:本题考查了直角三角形中勾股定理的运用,以及两边平方和等于第三边时可以判定直角三角形.
∴∠CAB=90°,
∴AC=
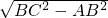 =
=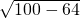 =6,
=6,∴S△BAC=
 AB•AC=24;
AB•AC=24;∵CD2+AD2=AC2,
∴△ACD为直角三角形,
∴S△ADC=
 AD•DC=
AD•DC= ;
;∴四边形ABCD的面积为
∴S△BAC+S△ADC=24+
 .
.答:四边形ABCD的面积为24+
 .
.分析:由CA⊥AB,可知∠CAB=90°,在Rt△ABC中运用勾股定理可以求AC的长度,因为AD2+DC2=AC2,所以△ACD为直角三角形,所以四边形ABCD的面积为Rt△ADC和Rt△BAC面积之和.
点评:本题考查了直角三角形中勾股定理的运用,以及两边平方和等于第三边时可以判定直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
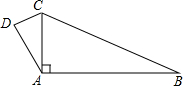 如图,CA⊥AB,AB=8,BC=10,DC=2,AD=
如图,CA⊥AB,AB=8,BC=10,DC=2,AD=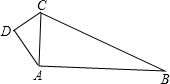 如图,CA⊥AB,AB=12,BC=13,DC=3,AD=4,求四边形ABCD的面积.
如图,CA⊥AB,AB=12,BC=13,DC=3,AD=4,求四边形ABCD的面积. 如图,CA⊥AB,垂足为点A,AB=12,AC=6,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=12,AC=6,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过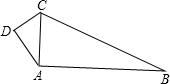
 ,求四边形ABCD的面积.
,求四边形ABCD的面积.