Question

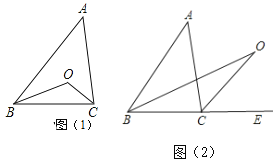
【题目】（1）如图（1）所示，已知在△ABC中，O为∠ABC和∠ACB的平分线BO，CO的交点．试猜想∠BOC和∠A的关系，并说明理由.

（2）如图（2）所示，若O为∠ABC的平分线BO和∠ACE的平分线CO的交点，则∠BOC与∠A的关系又该怎样？为什么？

Answer 1

【答案】(1)∠BOC=∠A+90°；理由见解析；(2)∠BOC=∠A；理由见解析

【解析】

试题分析：(1)、根据三角形内角和定理得出∠A+∠ABC+∠ACB=180°，∠BOC+∠OBC+∠OCB=180°，根据角平分线的性质得出∠ABC=2∠OBC，∠ACB=2∠OCB，然后得出∠BOC+∠ABC+∠ACB=180°，最后得出结论；(2)、根据外角的性质得出∠A+∠ABC=∠ACE，∠OBC+∠BOC=∠OCE，然后根据角平分线的性质得出∠ABC=2∠OBC，∠ACE=2∠OCE，最后根据∠BOC=∠OCE-∠OBC得出答案.

试题解析：(1)、∠BOC=∠A+90°．

在△ABC中，∠A+∠ABC+∠ACB=180°，在△BOC中，∠BOC+∠OBC+∠OCB=180°，

又∵ BO，CO分别是∠ABC，∠ACB的平分线， ∴ ∠ABC=2∠OBC，∠ACB=2∠OCB.

∴ ∠BOC+∠ABC+∠ACB=180°.

∴ ∠BOC=180°﹣(∠ABC+∠ACB)=180°-(180°-∠A)= 90°+∠A.

(2)、∠BOC=∠A．

∵ ∠A+∠ABC=∠ACE，∠OBC+∠BOC=∠OCE， ∴ ∠A=∠ACE-∠ABC, ∠BOC=∠OCE-∠OBC

又∵ BO，CO分别是∠ABC和∠ACE的平分线， ∴ ∠ABC=2∠OBC，∠ACE=2∠OCE.

∴∠BOC=∠OCE-∠OBC=∠ACE-∠ABC=(∠ACE-∠ABC)=∠A．