题目内容
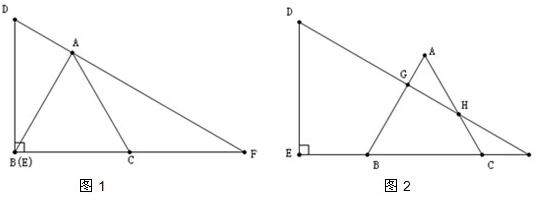
已知:△ABC是等边三角形,△BDC是等腰三角形,其中∠BDC=120°,过点D作∠EDF=60°,分别交AB于E,交AC于F,连接EF.
(1)若BE=CF,求证:①△DEF是等边三角形;②BE+CF=EF.
(2)若BE≠CF,即E、F分别是线段AB,AC上任意一点,BE+CF=EF还会成立吗?请说明理由.

(1)若BE=CF,求证:①△DEF是等边三角形;②BE+CF=EF.
(2)若BE≠CF,即E、F分别是线段AB,AC上任意一点,BE+CF=EF还会成立吗?请说明理由.

分析:(1)延长AB到N,使BN=CF,连接DN,求出∠FCD=∠EBD=∠NBD=90°,根据SAS证△EBD≌△FCD,推出ED=DF,得出等边三角形,根据SAS证△NBD≌△FCD,推出DN=DF,∠NDB=∠FDC,求出∠EDF=∠EDN,根据SAS证△EDF≌△EDN,推出EF=EN,即可得出答案;
(2)延长AB到N,使BN=CF,连接DN,求出∠FCD=∠EBD=∠NBD=90°,根据SAS证△NBD≌△FCD,推出DN=DF,∠NDB=∠FDC,求出∠EDF=∠EDN,根据SAS证△EDF≌△EDN,推出EF=EN,即可得出答案.
(2)延长AB到N,使BN=CF,连接DN,求出∠FCD=∠EBD=∠NBD=90°,根据SAS证△NBD≌△FCD,推出DN=DF,∠NDB=∠FDC,求出∠EDF=∠EDN,根据SAS证△EDF≌△EDN,推出EF=EN,即可得出答案.
解答:(1)证明:延长AB到N,使BN=CF,连接DN,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵△DBC是等腰三角形,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ACD=∠ABD=30°+60°=90°,
在△EBD和△FCD中
,
∴△EBD≌△FCD(SAS),
∴ED=DF,
∵∠EDF=60°,
∴△EDF是等边三角形,
∵△EBD≌△FCD,
∴∠EDB=∠FDC,
∵在△NBD和△FCD中
,
∴△NBD≌△FCD(SAS),
∴DN=DF,∠NDB=∠FDC,
∵∠EDB=∠FDC,
∴∠EDB=∠BDN=∠FDC,
∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,
∴∠EDB+∠BDN=60°,
即∠EDF=∠EDN,
在△EDN和△EDF中
,
∴△EDN≌△EDF(SAS),
∴EF=EN=BE+BN=BE+CF,
即△EDF是等边三角形,BE+CF=EF.
(2)解:BE+CF=EF还成立,理由是:
延长AB到N,使BN=CF,连接DN,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵△DBC是等腰三角形,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ACD=∠ABD=30°+60°=90°=∠NBD,
∵在△NBD和△FCD中
,
∴△NBD≌△FCD(SAS),
∴DN=DF,∠NDB=∠FDC,
∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,
∴∠EDB+∠BDN=60°,
即∠EDF=∠EDN,
在△EDN和△EDF中
,
∴△EDN≌△EDF(SAS),
∴EF=EN=BE+BN=BE+CF,
即BE+CF=EF.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵△DBC是等腰三角形,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ACD=∠ABD=30°+60°=90°,
在△EBD和△FCD中
|
∴△EBD≌△FCD(SAS),
∴ED=DF,
∵∠EDF=60°,
∴△EDF是等边三角形,
∵△EBD≌△FCD,
∴∠EDB=∠FDC,
∵在△NBD和△FCD中
|
∴△NBD≌△FCD(SAS),
∴DN=DF,∠NDB=∠FDC,
∵∠EDB=∠FDC,
∴∠EDB=∠BDN=∠FDC,
∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,
∴∠EDB+∠BDN=60°,
即∠EDF=∠EDN,
在△EDN和△EDF中
|
∴△EDN≌△EDF(SAS),
∴EF=EN=BE+BN=BE+CF,
即△EDF是等边三角形,BE+CF=EF.

(2)解:BE+CF=EF还成立,理由是:
延长AB到N,使BN=CF,连接DN,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵△DBC是等腰三角形,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ACD=∠ABD=30°+60°=90°=∠NBD,
∵在△NBD和△FCD中
|
∴△NBD≌△FCD(SAS),
∴DN=DF,∠NDB=∠FDC,
∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,
∴∠EDB+∠BDN=60°,
即∠EDF=∠EDN,
在△EDN和△EDF中
|
∴△EDN≌△EDF(SAS),
∴EF=EN=BE+BN=BE+CF,
即BE+CF=EF.
点评:本题考查了等边三角形性质和判定,等腰三角形的性质,三角形的内角和定理,全等三角形的性质和判定的综合运用,题目综合性比较强,有一定的难度,但是证明过程类似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
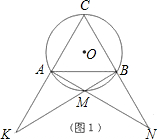

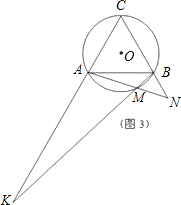
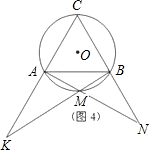
(1)如图1,图2,图3,M分别为
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
(2)如图4,当M为
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
已知,△ABC是等边三角形且内接于⊙O,取
 |
| AB |




(1)如图1,图2,图3,M分别为
 |
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 |
| AB |
(3)对(2)中提出的猜想,依图4给出证明.
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.