题目内容
(2009•内江)如图所示,已知点A(-1,0),B(3,0),C(0,t),且t>0,tan∠BAC=3,抛物线经过A、B、C三点,点P(2,m)是抛物线与直线l:y=k(x+1)的一个交点.(1)求抛物线的解析式;
(2)对于动点Q(1,m),求PQ+QB的最小值;
(3)若动点M在直线l上方的抛物线上运动,求△AMP的边AP上的高h的最大值.

【答案】分析:(1)根据题意可知tan∠BAC=3,所以可求得点C的坐标,根据待定系数法,即可求得二次函数的解析式;
(2)因为点P在抛物线上,所以可求得m的值,即可求得直线l的解析式,根据题意可得点Q在直线x=1上,可知点Q在抛物线的对称轴上,有两点间线段最短可知直线AP与抛物线的对称轴的交点即是点Q;求得AP的值即可;
(3)可首先求得△APM的最大值,利用图形面积的拼凑方法即可求得,再根据面积公式求得h的最大值即可.
解答:解:(1)∵tan∠BAC=3,
∴ =
= =3,
=3,
∴OC=3,
∴点C的坐标为(0,3),
∴t=3,
将点A、B、C的坐标代入二次函数解析式得: ,
,
解得: ,
,
∴此抛物线的解析式为y=-x2+2x+3;
(2)∵点P(2,m)在抛物线上,
∴m=3,
∴点P的坐标为(2,3),
∴3=3k,
∴k=1,
∴直线l的解析式为y=x+1,
∵y=-x2+2x+3=-(x-1)2+4,
∴此函数的对称轴为x=1,
∴点Q在抛物线的对称轴上,
∴点B关于对称轴的对称点为点A,
∴设直线AP的解析式为y=kx+b,
∴ ,
,
∴ ,
,
∴直线AP的解析式为y=x+1,
∴点Q的坐标为(1,2),
∴PQ+QB=PA= =3
=3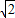 ;
;
(3)过点P作PN⊥x轴于点N,过点M作MK⊥x轴于点K,
设点M的坐标为(x,-x2+2x+3),
∴S△APM=S△AKM+S梯形PNKM-S△PNA,
= (1+x)(-x2+2x+3)+
(1+x)(-x2+2x+3)+ (-x2+2x+3+3)(2-x)-
(-x2+2x+3+3)(2-x)- ×3×3,
×3×3,
=- (x2-x-2),
(x2-x-2),
=- (x-
(x- )2+
)2+ ,
,
∴△APM的最大值为 ,
,
∵AP的长度不变,
∴△AMP的边AP上的高h的最大值为 .
.
点评:此题考查了二次函数的综合应用,要注意待定系数法球函数的解析式,还要注意利用二次函数求最大值,注意数形结合思想的应用.
(2)因为点P在抛物线上,所以可求得m的值,即可求得直线l的解析式,根据题意可得点Q在直线x=1上,可知点Q在抛物线的对称轴上,有两点间线段最短可知直线AP与抛物线的对称轴的交点即是点Q;求得AP的值即可;
(3)可首先求得△APM的最大值,利用图形面积的拼凑方法即可求得,再根据面积公式求得h的最大值即可.
解答:解:(1)∵tan∠BAC=3,
∴
 =
= =3,
=3,∴OC=3,
∴点C的坐标为(0,3),
∴t=3,
将点A、B、C的坐标代入二次函数解析式得:
 ,
,解得:
 ,
,∴此抛物线的解析式为y=-x2+2x+3;
(2)∵点P(2,m)在抛物线上,
∴m=3,
∴点P的坐标为(2,3),
∴3=3k,
∴k=1,
∴直线l的解析式为y=x+1,
∵y=-x2+2x+3=-(x-1)2+4,
∴此函数的对称轴为x=1,
∴点Q在抛物线的对称轴上,
∴点B关于对称轴的对称点为点A,
∴设直线AP的解析式为y=kx+b,

∴
 ,
,∴
 ,
,∴直线AP的解析式为y=x+1,
∴点Q的坐标为(1,2),
∴PQ+QB=PA=
 =3
=3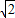 ;
;(3)过点P作PN⊥x轴于点N,过点M作MK⊥x轴于点K,
设点M的坐标为(x,-x2+2x+3),
∴S△APM=S△AKM+S梯形PNKM-S△PNA,
=
 (1+x)(-x2+2x+3)+
(1+x)(-x2+2x+3)+ (-x2+2x+3+3)(2-x)-
(-x2+2x+3+3)(2-x)- ×3×3,
×3×3,=-
 (x2-x-2),
(x2-x-2),=-
 (x-
(x- )2+
)2+ ,
,∴△APM的最大值为
 ,
,∵AP的长度不变,
∴△AMP的边AP上的高h的最大值为
 .
.点评:此题考查了二次函数的综合应用,要注意待定系数法球函数的解析式,还要注意利用二次函数求最大值,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



