题目内容
【题目】定义：我们把对角线相等的四边形叫做和美四边形．
请举出一种你所学过的特殊四边形中是和美四边形的例子．
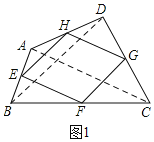
如图1，E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，已知四边形EFGH是菱形，求证：四边形ABCD是和美四边形；
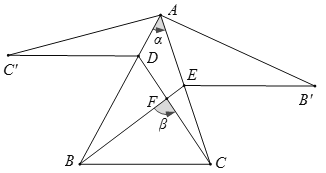
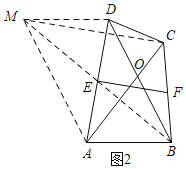
如图2，四边形ABCD是和美四边形，对角线AC，BD相交于O，
，E、F分别是AD、BC的中点，请探索EF与AC之间的数量关系，并证明你的结论．
【答案】（1）矩形；（2）证明见解析；（3）
，证明见解析.
【解析】
（1）等腰梯形、矩形、正方形，任选一个即可；
（2）根据三角形中位线性质可得
（3），连接BE并延长至M，使
，连接DM、AM、CM，先证四边形MABD是平行四边形，
，
，
，
是等边三角形，
，由三角形中位线性质得
．
解：
矩形的对角线相等，
矩形是和美四边形；
如图1，连接AC、BD，
，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，
，
，
四边形EFGH是菱形，
，
，
四边形ABCD是和美四边形；
，
证明：如图2，连接BE并延长至M，使，连接DM、AM、CM，
，
四边形MABD是平行四边形，
，，
，
是等边三角形，
，
中，
，
，
．
练习册系列答案
相关题目
