题目内容
(2001•北京)用换元法解方程: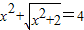 ,若设
,若设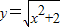 ,则原方程可化为 ;原方程的解为 .
,则原方程可化为 ;原方程的解为 .
【答案】分析:把方程整理后,设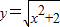 ,用换元法求解,注意检验.
,用换元法求解,注意检验.
解答:解:把方程整理得:x2+2+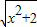 -6=0,设
-6=0,设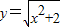 ,
,
原方程就化为y2+y-6=0,
(y+3)(y-2)=0,
解得y=-3或y=2,
经检验y=2是原方程的解.
∴x2+2=4,解得x=2或-2.
∴原方程的解为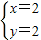 或
或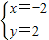 .
.
故本题答案为:y2+y-6=0;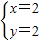 或
或 .
.
点评:所给方程较复杂,又都和某一代数式有关系时,可采用换元法使方程简便,注意无理方程需验根.
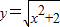 ,用换元法求解,注意检验.
,用换元法求解,注意检验.解答:解:把方程整理得:x2+2+
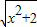 -6=0,设
-6=0,设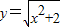 ,
,原方程就化为y2+y-6=0,
(y+3)(y-2)=0,
解得y=-3或y=2,
经检验y=2是原方程的解.
∴x2+2=4,解得x=2或-2.
∴原方程的解为
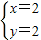 或
或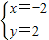 .
.故本题答案为:y2+y-6=0;
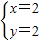 或
或 .
.点评:所给方程较复杂,又都和某一代数式有关系时,可采用换元法使方程简便,注意无理方程需验根.

练习册系列答案
相关题目


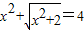 ,若设
,若设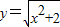 ,则原方程可化为 ;原方程的解为 .
,则原方程可化为 ;原方程的解为 .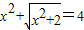 ,若设
,若设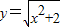 ,则原方程可化为 ;原方程的解为 .
,则原方程可化为 ;原方程的解为 .