题目内容
阅读:如图(1),正方形ABCD的边AB在x轴上,C、D在抛物线y=-x(x-2)的图象上,我们称正方形ABCD内接于抛物线y=-x(x-2).抛物线y=-x(x-2)的对称轴交x轴于点M,设正方形ABCD的边长为a1,那么a1满足哪个二元一次方程呢?由对称性可知M是AB的中点,则AM=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)如图(2),若并排两个正方形内接于抛物线y=-x(x-2),则每个正方形的边长a2满足的二元一次方程是
(2)如图(3),若并排三个正方形内接于抛物线y=-x(x-2),则每个正方形的边长a3满足的二元一次方程是
(3)如图(4),若并排n个正方形内接于抛物线y=-x(x-2),则每个正方形的边长an满足的二元一次方程是
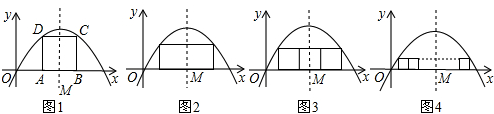
分析:根据图1的解题方法,根据抛物线、正方形的对称性求出D点坐标,代入抛物线解析式,变形即可.
解答:解:(1)∵每个正方形的边长a2,
∴由对称性可知M是AB的中点,则AM=a2,AD=a2,易知OM=1,所以OA=1-a2,所以D点坐标为(1-a2,a2),
代入抛物线解析式y=-x(x-2),得-(1-a2)(1-a2-2)=a2,整理得a22+a2-1=0,
即a2满足二元一次方程(
)2a22+a2-1=0;
(2)同理,得(
)2a32+a3-1=0;
(3)由此,得(
)2an2+an-1=0.
∴由对称性可知M是AB的中点,则AM=a2,AD=a2,易知OM=1,所以OA=1-a2,所以D点坐标为(1-a2,a2),
代入抛物线解析式y=-x(x-2),得-(1-a2)(1-a2-2)=a2,整理得a22+a2-1=0,
即a2满足二元一次方程(
| 2 |
| 2 |

(2)同理,得(
| 3 |
| 2 |
(3)由此,得(
| n |
| 2 |
点评:本题考查了二次函数的综合运用.关键是通过材料的阅读,得出解题方法,进一步推出一般结论.

练习册系列答案
相关题目

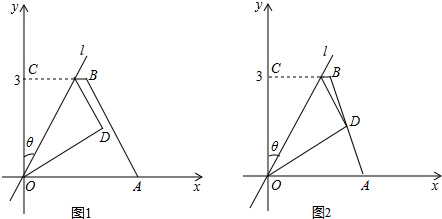
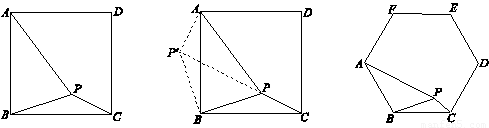
 ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数. ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
 ,PB=
,PB=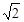 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数. ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为
.
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为
.
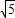 ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数. ,PB=4,PC=2,则∠BPC的度数为______,正六边形ABCDEF的边长为______
,PB=4,PC=2,则∠BPC的度数为______,正六边形ABCDEF的边长为______