题目内容
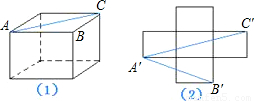
(2005•芜湖)如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示.已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出最长线段的长度这样的线段可画几条?
(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系?
【答案】分析:(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长,又因为展开图形中有两个长方形,每个长方形有两条对角线,知这样的线段可画4条;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
解答:解:(1)在平面展开图中可画出最长的线段长为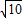 ,(1分)
,(1分)
如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴ .(3分)
.(3分)
答:这样的线段可画4条(另三条用虚线标出).(4分)

(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,∴∠BAC=45°.(5分)
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'= ,B'C'=
,B'C'= .(7分)
.(7分)
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,∴△A′B′C′为等腰直角三角形.(8分)
∴∠B′A′C′=45°.(9分)
∴∠BAC与∠B′A′C′相等.(10分)
点评:本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
解答:解:(1)在平面展开图中可画出最长的线段长为
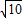 ,(1分)
,(1分)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴
 .(3分)
.(3分)答:这样的线段可画4条(另三条用虚线标出).(4分)

(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,∴∠BAC=45°.(5分)
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=
 ,B'C'=
,B'C'= .(7分)
.(7分)又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,∴△A′B′C′为等腰直角三角形.(8分)
∴∠B′A′C′=45°.(9分)
∴∠BAC与∠B′A′C′相等.(10分)
点评:本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.

练习册系列答案
相关题目
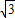 ,求AD的长度.
,求AD的长度.
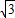 ,则坡角α为( )
,则坡角α为( )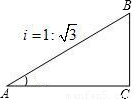

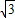 ,求AD的长度.
,求AD的长度.