题目内容
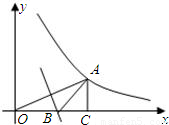
(2010•南安市质检)如图,已知点A在双曲线y=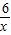 上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积= ;△ABC的周长为 .
上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积= ;△ABC的周长为 .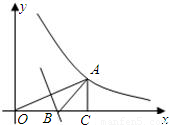
【答案】分析:首先由反比例函数比例系数k的几何意义,直接得出△AOC的面积= |k|=3;
|k|=3;
如果设A(x,y),那么由线段垂直平分线的性质可知AB=OB,则△ABC的周长=OC+AC=x+y.由点A在双曲线y= 上,且OA=4,可列出方程组,运用完全平方公式将方程组变形,求出x+y的值,从而得出结果.
上,且OA=4,可列出方程组,运用完全平方公式将方程组变形,求出x+y的值,从而得出结果.
解答:解:∵点A在双曲线y= 上,过A作AC⊥x轴于C,
上,过A作AC⊥x轴于C,
∴△AOC的面积= |k|=3;
|k|=3;
设点A的坐标为(x,y).
∵点A在第一象限,
∴x>0,y>0.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=x+y.
∵点A在双曲线y=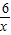 上,且OA=4,
上,且OA=4,
∴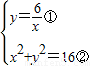
由①得,xy=6③,
③×2+②,得x2+2xy+y2=28,
∴(x+y)2=28,
∵x>0,y>0,
∴x+y=2 .
.
∴△ABC的周长=2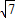 .
.
故答案为:3,2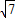 .
.
点评:此题综合考查了反比例函数的性质,线段垂直平分线的性质,完全平方公式等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.
 |k|=3;
|k|=3;如果设A(x,y),那么由线段垂直平分线的性质可知AB=OB,则△ABC的周长=OC+AC=x+y.由点A在双曲线y=
 上,且OA=4,可列出方程组,运用完全平方公式将方程组变形,求出x+y的值,从而得出结果.
上,且OA=4,可列出方程组,运用完全平方公式将方程组变形,求出x+y的值,从而得出结果.解答:解:∵点A在双曲线y=
 上,过A作AC⊥x轴于C,
上,过A作AC⊥x轴于C,∴△AOC的面积=
 |k|=3;
|k|=3;设点A的坐标为(x,y).
∵点A在第一象限,
∴x>0,y>0.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=x+y.
∵点A在双曲线y=
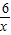 上,且OA=4,
上,且OA=4,∴
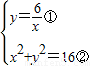
由①得,xy=6③,
③×2+②,得x2+2xy+y2=28,
∴(x+y)2=28,
∵x>0,y>0,
∴x+y=2
 .
.∴△ABC的周长=2
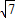 .
.故答案为:3,2
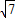 .
.点评:此题综合考查了反比例函数的性质,线段垂直平分线的性质,完全平方公式等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
相关题目
 上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积= ;△ABC的周长为 .
上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积= ;△ABC的周长为 .