题目内容
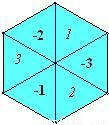
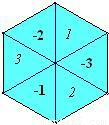
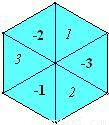
如图，正六边形的游戏盘被分成6个面积相等的三角形，每一个三角形都标有相应的数字．甲乙两人按一定的距离分别向盘中投镖一次，设甲、乙两人投掷的飞镖扎在的区域内的数字分别为x和y．（若飞镖
扎在边界线上时，重投一次，直到指向一个区域为止）
（1）直接写出甲投掷飞镖所扎区域内的数字x为正数的概率；
（2）求出点（x，y）落在第一象限内的概率，并说明理由．
解：（1）∵除了负数就是正数就这两种情况，∴P（正数）=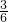
=
；
（2）根据题意，画表格或画树状图或列举法说明均可，
由上图可知，点（x，y）的坐标共有36种等可能的结果，
其中点（x，y）落在第一象限的共有9种，
所以，P（点（x，y）落在第一象限）=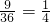
．
分析：（1）根据几何概率的特点，6个三角形面积相等，面积比即为概率；
（2）要熟悉各象限内坐标的特点．找到第一象限点的情况数占总情况数的多少即可．
点评：用到的知识点为：概率=所求情况数与总情况数之比．第一象限点的符号为（+，+）．
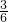=；（2）根据题意，画表格或画树状图或列举法说明均可，
| 甲 乙 | 1 | 2 | 3 | -1 | -2 | -3 |
| 1 | （1，1） | （2，1） | （3，1） | （-1，1） | （-2，1） | （-3，1） |
| 2 | （1，2） | （2，2） | （3，2） | （-1，2） | （-2，2） | （-3，2） |
| 3 | （1，3） | （2，3） | （3，3） | （-1，3） | （-2，3） | （-3，3） |
| -1 | （1，-1） | （2，-1） | （3，-1） | （-1，-1） | （-2，-1） | （-3，-1） |
| -2 | （1，-2） | （2，-2） | （3，-2） | （-1，-2） | （-2，-2） | （-3，-2） |
| -3 | （1，-3） | （2，-3） | （3，-3） | （-1，-3） | （-2，-3） | （-3，-3） |
其中点（x，y）落在第一象限的共有9种，
所以，P（点（x，y）落在第一象限）=
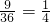．分析：（1）根据几何概率的特点，6个三角形面积相等，面积比即为概率；
（2）要熟悉各象限内坐标的特点．找到第一象限点的情况数占总情况数的多少即可．
点评：用到的知识点为：概率=所求情况数与总情况数之比．第一象限点的符号为（+，+）．
练习册系列答案
全能测控期末小状元系列答案
相关题目
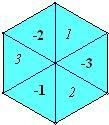扎在边界线上时，重投一次，直到指向一个区域为止）
