Question

圆内一条弦与直径相交成30°且分这条直径为1cm和5cm，则圆心到这条弦的距离为________cm．

Answer 1

1
分析：过O作OF⊥CD于F，则OF的长是圆心到这条弦的距离，求出OA、OE的长，根据含30度角的直角三角形性质求出OF即可．
解答：过O作OF⊥CD于F，
则OF的长是圆心到这条弦的距离，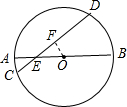
AB=1cm+5cm=6cm，
∴OA=OB=3cm，
∴OE=3cm-1cm=2cm，
∵∠FEO=30°，∠OFE=90°，
∴OF=OE=1cm．
故答案为：1．
点评：本题考查了切线的性质和含30度角的直角三角形的性质的应用，关键是求出OE长和得出OF=OE，主要培养学生运用性质进行推理的能力．