题目内容
 如图,已知AB∥EF∥DC,EG∥BD,则图中与∠ABD互为补角的共有
如图,已知AB∥EF∥DC,EG∥BD,则图中与∠ABD互为补角的共有
- A.3个
- B.4个
- C.1个
- D.2个
A
分析:根据平行线性质得出∠ABD+∠FHB=180°,∠ABD+∠FGB=180°,根据对顶角相等得出∠ABD+∠DHE=180°,即可得出答案.
解答:∵AB∥EF∥DC,
∴∠ABD+∠FHB=180°,
∵∠DHE=∠FHB,
∴∠ABD+∠DHE=180°,
∵EG∥BD,
∴∠ABD+∠FGB=180°,
∴与∠ABD互补的角有∠FHB,∠DHE,∠FGB,共3个,
故选A.
点评:本题考查了邻补角和平行线的性质,注意:平行线性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.
分析:根据平行线性质得出∠ABD+∠FHB=180°,∠ABD+∠FGB=180°,根据对顶角相等得出∠ABD+∠DHE=180°,即可得出答案.
解答:∵AB∥EF∥DC,
∴∠ABD+∠FHB=180°,
∵∠DHE=∠FHB,
∴∠ABD+∠DHE=180°,
∵EG∥BD,
∴∠ABD+∠FGB=180°,
∴与∠ABD互补的角有∠FHB,∠DHE,∠FGB,共3个,
故选A.
点评:本题考查了邻补角和平行线的性质,注意:平行线性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.

练习册系列答案
相关题目
 14、如图,已知AB∥EF,∠C=40°,∠CDF=30°,则∠B=
14、如图,已知AB∥EF,∠C=40°,∠CDF=30°,则∠B=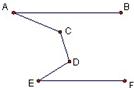
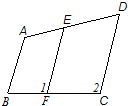 26、如图,已知AB∥EF,∠1=∠2,那么AB与CD平行吗?为什么?请说明理由.
26、如图,已知AB∥EF,∠1=∠2,那么AB与CD平行吗?为什么?请说明理由.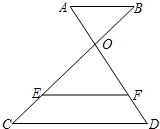 如图,已知AB∥EF∥CD,AD与BC相交于点O.
如图,已知AB∥EF∥CD,AD与BC相交于点O.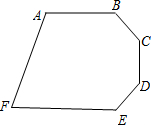 如图,已知AB∥EF,若α=∠A+∠F,β=∠B+∠C+∠D+∠E,试探究β与α之间的数量关系,并证明你的结论.
如图,已知AB∥EF,若α=∠A+∠F,β=∠B+∠C+∠D+∠E,试探究β与α之间的数量关系,并证明你的结论.