题目内容
【题目】如图，在坡角为30°的山坡上有一铁塔AB，其正前方矗立着一大型广告牌，当阳光与水平线成45°角时，测得铁塔AB落在斜坡上的影子BD的长为6米，落在广告牌上的影子CD的长为4米，求铁塔AB的高（AB，CD均与水平面垂直，结果保留根号）．
【答案】解：过点C作CE⊥AB于E，过点B作BF⊥CD于F，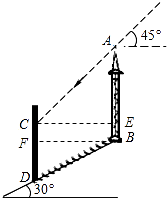
在Rt△BFD中，
∵∠DBF=30°，sin∠DBF= 
= 
，cos∠DBF= 
= 
，
∵BD=6，
∴DF=3，BF=3 
，
∵AB∥CD，CE⊥AB，BF⊥CD，
∴四边形BFCE为矩形，
∴BF=CE=3 ，CF=BE=CD﹣DF=1，
在Rt△ACE中，∠ACE=45°，
∴AE=CE=3 ，
∴AB=3 +1．
答：铁塔AB的高为（3 +1）m．
【解析】过点C作CE⊥AB于E，过点B作BF⊥CD于F，在Rt△BFD中，分别求出DF、BF的长度，在Rt△ACE中，求出AE、CE的长度，继而可求得AB的长度．
互动课堂系列答案【题目】2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示： 
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案： ①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
赠送话费（单位：元） | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查，记X（单位：元）为该市民参加问卷调查获赠的话费，求X的分布列．
附： 
≈14.5
若Z～N（μ，δ2），则P（μ﹣δ＜Z＜μ+δ）=0.6826，P（μ﹣2δ＜Z＜μ+2δ）=0.9544．
