题目内容
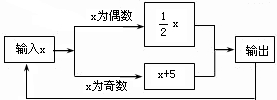
(2012•保定一模)四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.
(1)如图2,画出菱形ABCD的一个准等距点.
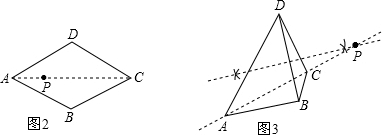
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
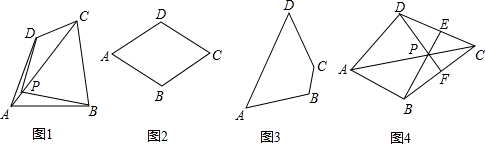
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.

分析:(1)根据菱形的性质,在菱形对角线上找出除中心外的任意一点即可;
(2)作对角线BD的垂直平分线于与另一对角线AC相交于点P,根据线段垂直平分线上的点到线段两端点的距离相等可得点P即为所求的准等距点;
(3)连接BD,先利用“角角边”证明△DCF和△BCE全等,根据全等三角形对应边相等可得CD=CB,再根据等边对等角的性质可得∠CDB=∠CBD,从而得到∠PDB=∠PBD,然后根据等角对等边的性质可得PD=PB,根据准等距点的定义即可得证.
(2)作对角线BD的垂直平分线于与另一对角线AC相交于点P,根据线段垂直平分线上的点到线段两端点的距离相等可得点P即为所求的准等距点;
(3)连接BD,先利用“角角边”证明△DCF和△BCE全等,根据全等三角形对应边相等可得CD=CB,再根据等边对等角的性质可得∠CDB=∠CBD,从而得到∠PDB=∠PBD,然后根据等角对等边的性质可得PD=PB,根据准等距点的定义即可得证.
解答:解:(1)如图2,点P即为所画点.…(1分)(答案不唯一)
(2)如图3,点P即为所作点.…(2分)(答案不唯一.)
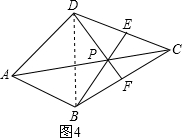
(3)证明:连接DB,
在△DCF与△BCE中,
,
∴△DCF≌△BCE(AAS),
∴CD=CB,
∴∠CDB=∠CBD.
∴∠PDB=∠PBD,
∴PD=PB,
∵PA≠PC
∴点P是四边形ABCD的准等距点.
(2)如图3,点P即为所作点.…(2分)(答案不唯一.)


(3)证明:连接DB,
在△DCF与△BCE中,
|
∴△DCF≌△BCE(AAS),
∴CD=CB,
∴∠CDB=∠CBD.
∴∠PDB=∠PBD,
∴PD=PB,
∵PA≠PC
∴点P是四边形ABCD的准等距点.
点评:本题考查了复杂作图,主要利用了线段垂直平分线的作法,全等三角形的判定与性质,读懂题意,理解准等距点的定义是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
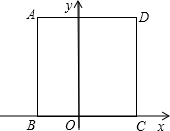 (2012•保定一模)如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点D的坐标是(3,4),则点B的坐标是
(2012•保定一模)如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点D的坐标是(3,4),则点B的坐标是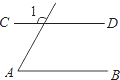 (2012•保定一模)如图,已知AB∥CD,∠1=100°,则∠A的度数是( )
(2012•保定一模)如图,已知AB∥CD,∠1=100°,则∠A的度数是( )