题目内容
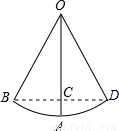
如图是一个小孩荡秋千的示意图,秋千链子OB的长度为2米,当秋千向两边摆动时,摆角∠BOD恰好为60°,且两边的摆动角度相同,则它摆至最高位置时与其摆至最低位置时的高度之差AC是( )
A.(2-
 )米
)米B.
 米
米C.(2-
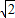 )米
)米D.
 米
米
【答案】分析:由题意知,秋千摆至最低点时,点A为弧BD的中点,由垂径定理知BD⊥OA,BC=DC.再根据等边三角形的性质求得OC即可.
解答:解:∵点A为弧BD的中点,O为圆心
由垂径定理知:BD⊥OA,BC=DC,弧AB=弧AD
∵∠BOD=60°
∴∠BOA=30°
∵OB=OA=OD=2
∴CB=1
在Rt△OBC中,根据勾股定理,知OC=
∴AC=OA-OC=2-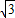
故选A.
点评:本题需根据题意,将实际问题抽象为几何问题,再利用垂径定理和等边三角形的性质解答.
解答:解:∵点A为弧BD的中点,O为圆心
由垂径定理知:BD⊥OA,BC=DC,弧AB=弧AD
∵∠BOD=60°
∴∠BOA=30°
∵OB=OA=OD=2
∴CB=1
在Rt△OBC中,根据勾股定理,知OC=

∴AC=OA-OC=2-
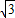
故选A.
点评:本题需根据题意,将实际问题抽象为几何问题,再利用垂径定理和等边三角形的性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
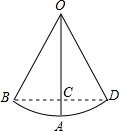 如图是一个小孩荡秋千的示意图,秋千链子OB的长度为2米,当秋千向两边摆动时,摆角∠BOD恰好
如图是一个小孩荡秋千的示意图,秋千链子OB的长度为2米,当秋千向两边摆动时,摆角∠BOD恰好为60°,且两边的摆动角度相同,则它摆至最高位置时与其摆至最低位置时的高度之差AC是( )
A、(2-
| ||||
B、
| ||||
C、(2-
| ||||
D、
|

 )米
)米 米
米 )米
)米 米
米
 )米
)米 米
米 )米
)米 米
米
 )米
)米 米
米 )米
)米 米
米