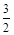题目内容
若m+n=2,mn=1,则(1-m)(1-n)的值为
| A.0 | B.1 | C.2 | D.3 |
A
先根据多项式乘以多项式运算法则把(1-m)(1-n)化简,再把m+n=2,mn=1整体代入化简的结果即可得问题的答案.
解:∵(1-m)(1-n)
=1-n-m+mn
=1-(m+n)+mn,
又∵m+n=2,mn=1,
∴原式=1-2+1=0.
故选A.
本题考查了整式的化简求值,先按运算顺序把整式化简,再把对应字母的值代入求整式的值;有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
解:∵(1-m)(1-n)
=1-n-m+mn
=1-(m+n)+mn,
又∵m+n=2,mn=1,
∴原式=1-2+1=0.
故选A.
本题考查了整式的化简求值,先按运算顺序把整式化简,再把对应字母的值代入求整式的值;有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
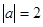 ,
, ,则
,则 为( )
为( )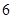

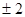
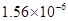 米,那么它的一百万倍相当于( )
米,那么它的一百万倍相当于( ) ,则“
,则“ ”内应填的实数是
”内应填的实数是