题目内容
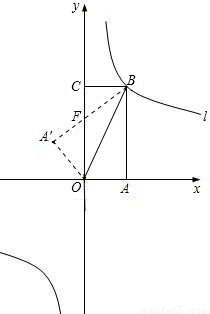
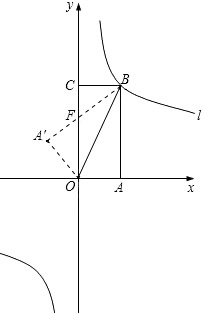
如图,矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴,y轴上,连接OB,将纸片OABC沿BC折叠,使点A落在点A′处,A′B与y轴交于点F,已知OA=1,AB=2。
(1)设CF=x,则OF=_____;
(2)求BF的长;
(3)设过点B的双曲线为l,试问双曲线l上是否存在一点M,使得以OB为一边的△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由。
(2)求BF的长;
(3)设过点B的双曲线为l,试问双曲线l上是否存在一点M,使得以OB为一边的△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由。
解:(1)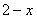 ;
;
(2)由轴对称的性质可知:∠FBO=∠OBA
在矩形OABC中,OC∥AB,则∠FOB=∠OBA
∴∠FBO=∠OBA
∴BF=OF=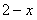
在Rt△FCB中,BC=OA=1,由勾股定理可得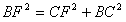
即: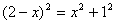
解得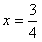
则BF=OF=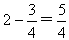 。
。
(3)设双曲线l的解析式为: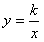
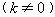
又过点B(1,2)
∴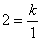 ,
,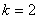
∴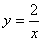
因为S△OAB=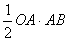 =
=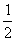 ×1×2=1
×1×2=1
∴S△COB=S△A′OB=1
∴双曲线l上符合条件的点M,应在与OB平行且距离等于点C到OB的距离的直线上。
直线OB过点(0,0),(1,2)
直线OB的解析式为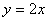 ,则过点C与OB平行的直线为:
,则过点C与OB平行的直线为: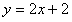
点M可能是过点C且与OB平行的直线与双曲线的交点
由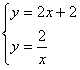 ,解得
,解得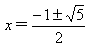
由轴对称性可知,点M可能是过点A且与OB平行的直线与双曲线l的交点
由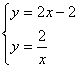 ,解得:
,解得: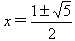
综上,符合条件的点M的横坐标是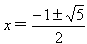 或x=
或x=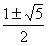 。
。

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
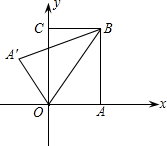 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=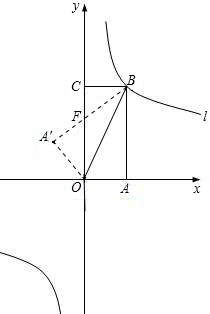 如图,矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴,y轴上,连接OB,将纸片OABC沿BC折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.
如图,矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴,y轴上,连接OB,将纸片OABC沿BC折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.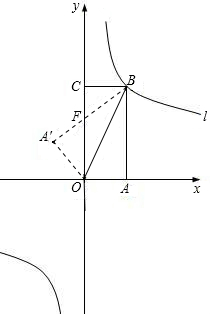 如图,矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴,y轴上,连接OB,将纸片OABC沿BC折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.
如图,矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴,y轴上,连接OB,将纸片OABC沿BC折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.