题目内容
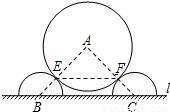
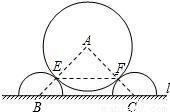
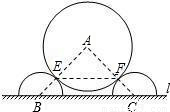
如图是某城市一个主题雕塑的平面示意图，它由置放于地面l上两个半径均为2米的半圆与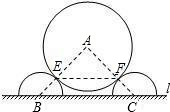
半径为4米的⊙A构成．点B、C分别是两个半圆的圆心，⊙A分别与两个半圆相切于点E、F，BC长为8米．求EF的长．
分析：由各圆的半径可得到AE=AF=4，BE=CF=2，AB=AC=6．则由两边对应成比例，且夹角相等得到△AEF∽△ABC．故
=
．则可求得EF的值．
| EF |
| BC |
| AE |
| AB |
解答：解：∵⊙A分别与两个半圆相切于点E、F，点A、B、C分别是三个圆的圆心，
∴AE=AF=4米，BE=CF=2米，AB=AC=6米．
则在△AEF和△ABC中，∠EAF=∠BAC，
=
=
=
，
∴△AEF∽△ABC．
故
=
，则EF=BC•
=8×
=
（米）．
∴AE=AF=4米，BE=CF=2米，AB=AC=6米．
则在△AEF和△ABC中，∠EAF=∠BAC，
| AE |
| AB |
| AF |
| AC |
| 4 |
| 6 |
| 2 |
| 3 |
∴△AEF∽△ABC．
故
| EF |
| BC |
| AE |
| AB |
| AE |
| AB |
| 2 |
| 3 |
| 16 |
| 3 |
点评：本题主要考查了圆与圆的位置关系以及相似三角形的判定和性质．
练习册系列答案
相关题目
