题目内容
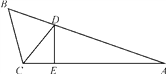
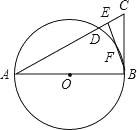
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=![]() ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC=![]() ,求AC的长.
,求AC的长.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)首先连接AF,由AB为直径,根据圆周角定理,可得∠AFB=90°,又由AE=AB,∠EBC=![]() ∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;
∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;
(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)连接AF.
∵AB为直径,
∴∠AFB=90°.
∵AE=AB,
∴△ABE为等腰三角形.
∴∠BAF=![]() ∠BAC.
∠BAC.
∵∠EBC=![]() ∠BAC,
∠BAC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.
即AB⊥BC,
∴BC与⊙O相切.

(2)过E作EG⊥BC于点G,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC=![]() .
.
在△AFB中,∠AFB=90°,
∵AB=8,
∴BF=ABsin∠BAF=8×![]() =2,
=2,
∴BE=2BF=4.
在△EGB中,∠EGB=90°,
∴EG=BEsin∠EBC=4×![]() =1,
=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴![]() .
.
∴![]() ,
,
∴CE=![]() ,
,
∴AC=AE+CE=8+![]() =
=![]() .
.


【题目】长春南溪湿地公园总占地面积约为3 100 000平方米.3 100 000这个数用科学记数法表示为( )
A. 3.1×105 B. 3.1×106 C. O.31×107 D. 3.1×107
【题目】九年级二班45名同学在学校举行的“爱心涌动校园”募捐活动中捐款情况如下表:
捐款数(元) | 10 | 20 | 30 | 40 | 50 |
捐款人数(人) | 8 | 17 | 16 | 2 | 2 |
则全班捐款的45个数据众数和中位数是( )
A. 20元,30元B. 50元,30元C. 50元,20元D. 20元,20元