题目内容
 如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为
如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为 (即tan∠PAB=
(即tan∠PAB= ,其中PB⊥AB),且O、A、B在同一条直线上.
,其中PB⊥AB),且O、A、B在同一条直线上.
(1)求此高层建筑的高度OC;
(2)求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度.(人的高度及测量仪器高度忽略不计,结果保留根号形式)
 解:(1)Rt△OAC中,∠OAC=60°,OA=50米,
解:(1)Rt△OAC中,∠OAC=60°,OA=50米,∴OC=OA•tan60°=50
 米.
米.答:此高层建筑的高度OC为50
 米.
米.(2)过P作PM⊥OC于M.
Rt△PMC中,∠CPM=45°,则PM=CM.
Rt△PBA中,tan∠PAB=
 .
.设PB=x,则AB=2x.
CM=OC-OM=50
 -x,PM=OA+AB=50+2x.
-x,PM=OA+AB=50+2x.∴50
 -x=50+2x,
-x=50+2x,即x=
 .
.∵AB=2x,AP=
 =
=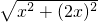 =
= x,
x,∴AB=
 (米),
(米),AP=
 (米).
(米).答:坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度为
 (米).
(米).分析:(1)在Rt△OAC中,易知∠OAC的度数,通过解直角三角形即可得到OC的长;
(2)过P作OC的垂线,设垂足为M.在Rt△PMC中,易知∠CPM=45°,则CM=PM.可用PB分别表示出CM、PM的长,进而根据CM=PM得到关于PB的等量关系式,据此求出PB的长,然后在Rt△PAB中,根据勾股定理求得斜坡AP的长度.
点评:此题主要考查学生对坡度坡角的掌握及三角函数的运用能力.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
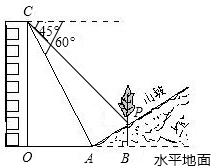 如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为
如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为
 (即tan∠PAB=
(即tan∠PAB=
 (即tan∠PAB=
(即tan∠PAB=
 (即tan∠PAB=
(即tan∠PAB=