题目内容
(2011•峨山县模拟)如图,在平面直角坐标系中,点M在X轴上,⊙M与Y轴相切于O点,过点A(2,0)作⊙M的切线,切点为B点,已知: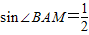 .
.(1)求⊙M的半径r;
(2)求点B的坐标;
(3)若抛物线y=ax2+bx+c经过点A、B、M三点,求此抛物线的解析式;
(4)在y轴上是否存在点C,使△ABC为直角三角形?若存在,请求出C点的坐标;若不存在,请说明理由.

【答案】分析:(1)可连接BM,根据sin∠A的正弦值,可得出BM:AM=1:2,也就是AM=2BM=OM+OA=BM+OA,因此BM=OA,即可求出r的值.
(2)可过B作BN⊥AM于N,那么ON就是B的横坐标的绝对值,BN就是B的纵坐标.在直角三角形BMN中,已求的了半径的长,又可求得∠BMA=60°,即可求出BN,MN的长,也就求出了ON的长,进而可得出B点的坐标.
(3)已经求的了A,B,M的坐标,可用待定系数法求二次函数的解析式(可用交点式的二次函数通式来设二次函数)
(4)要分三种情况进行讨论:
①当∠ABC=90°时,那么C点就在BM所在直线上,可在直角三角形MOC中,根据OM和∠CMO的度数求出OC的长,即可得出C的坐标.
②当∠BAC=90°时,那么∠OAC=60°,在直角三角形OAC中可根据OA的长求出OC的长,也就得出了C点的坐标
③当∠BCA=90°时,那么AB是斜边,可设出C的坐标,然后用坐标系中两点的距离公式分别表示出AC2,BC2,AB2,然后根据勾股定理即可求出C的坐标.
解答: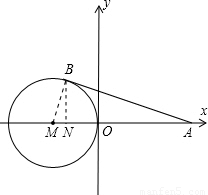 解:(1)连接BM,则∠MBA=90°.
解:(1)连接BM,则∠MBA=90°.
直角三角形MBA中,sin∠A=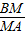 =
= ,BM=r,MA=OM+AO=r+2.
,BM=r,MA=OM+AO=r+2.
因此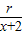 =
= ,r=2.
,r=2.
(2)过B作BN⊥AM于N,
∵sin∠A=30°
∴∠A=∠MBN=30°,∠BMN=60°
直角三角形BMN中,BM=2,∠BMN=60°,
因此MN=1,BN=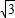 .
.
∴ON=OM-MN=1
因此B的坐标是(-1,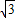 ).
).
(3)由于OM=2,
因此M的坐标是(-2,0).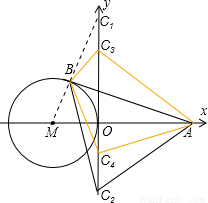
设抛物线的解析式为y=a(x-2)(x+2),
由于抛物线过B(-1,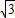 )
)
可得:a(1-4)=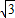 ,a=-
,a=-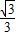
因此抛物线的解析式为y=-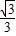 x2+
x2+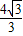 .
.
(4)可分三种情况:
①当∠ABC=90°时,C在直线BM上,
直角三角形MCO中,∠CMO=60°,OM=2,
因此OC=2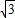 ,即C点的坐标为(0,2
,即C点的坐标为(0,2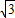 )
)
②当∠BAC=90°时,那么∠OAC=90°-∠BAM=60°,直角三角形OAC中
OC=OA•tan60°=2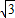 ,即C点的坐标为(0,-2
,即C点的坐标为(0,-2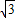 )
)
③当∠BCA=90°时,设C点坐标为(0,y),则
AC2=4+y2,BC2=(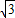 -y)2+1,AB2=3+9=12,
-y)2+1,AB2=3+9=12,
根据勾股定理可得:BC2+AC2=AB2
4+y2+(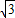 -y)2+1=12,
-y)2+1=12,
解得y=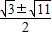 ,
,
综上所述,C点的坐标应该是(0,±2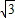 )和(0,
)和(0,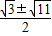 ).
).
点评:本题结合圆,三角形的知识考查了二次函数的综合应用,结合几何知识,利用数形结合的思想求解是这类题的基本思路.要注意(4)中要分情况进行讨论,不要漏解.
(2)可过B作BN⊥AM于N,那么ON就是B的横坐标的绝对值,BN就是B的纵坐标.在直角三角形BMN中,已求的了半径的长,又可求得∠BMA=60°,即可求出BN,MN的长,也就求出了ON的长,进而可得出B点的坐标.
(3)已经求的了A,B,M的坐标,可用待定系数法求二次函数的解析式(可用交点式的二次函数通式来设二次函数)
(4)要分三种情况进行讨论:
①当∠ABC=90°时,那么C点就在BM所在直线上,可在直角三角形MOC中,根据OM和∠CMO的度数求出OC的长,即可得出C的坐标.
②当∠BAC=90°时,那么∠OAC=60°,在直角三角形OAC中可根据OA的长求出OC的长,也就得出了C点的坐标
③当∠BCA=90°时,那么AB是斜边,可设出C的坐标,然后用坐标系中两点的距离公式分别表示出AC2,BC2,AB2,然后根据勾股定理即可求出C的坐标.
解答:
 解:(1)连接BM,则∠MBA=90°.
解:(1)连接BM,则∠MBA=90°.直角三角形MBA中,sin∠A=
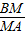 =
= ,BM=r,MA=OM+AO=r+2.
,BM=r,MA=OM+AO=r+2.因此
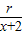 =
= ,r=2.
,r=2.(2)过B作BN⊥AM于N,
∵sin∠A=30°
∴∠A=∠MBN=30°,∠BMN=60°
直角三角形BMN中,BM=2,∠BMN=60°,
因此MN=1,BN=
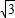 .
.∴ON=OM-MN=1
因此B的坐标是(-1,
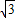 ).
).(3)由于OM=2,
因此M的坐标是(-2,0).

设抛物线的解析式为y=a(x-2)(x+2),
由于抛物线过B(-1,
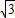 )
)可得:a(1-4)=
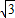 ,a=-
,a=-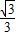
因此抛物线的解析式为y=-
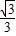 x2+
x2+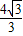 .
.(4)可分三种情况:
①当∠ABC=90°时,C在直线BM上,
直角三角形MCO中,∠CMO=60°,OM=2,
因此OC=2
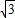 ,即C点的坐标为(0,2
,即C点的坐标为(0,2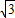 )
)②当∠BAC=90°时,那么∠OAC=90°-∠BAM=60°,直角三角形OAC中
OC=OA•tan60°=2
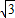 ,即C点的坐标为(0,-2
,即C点的坐标为(0,-2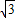 )
)③当∠BCA=90°时,设C点坐标为(0,y),则
AC2=4+y2,BC2=(
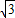 -y)2+1,AB2=3+9=12,
-y)2+1,AB2=3+9=12,根据勾股定理可得:BC2+AC2=AB2
4+y2+(
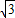 -y)2+1=12,
-y)2+1=12,解得y=
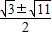 ,
,综上所述,C点的坐标应该是(0,±2
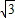 )和(0,
)和(0,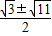 ).
).点评:本题结合圆,三角形的知识考查了二次函数的综合应用,结合几何知识,利用数形结合的思想求解是这类题的基本思路.要注意(4)中要分情况进行讨论,不要漏解.

练习册系列答案
相关题目
 .
.
 (2011•峨山县模拟)如图,在平面直角坐标系中,直线L:y=x是第一、三象限的角平分线.
(2011•峨山县模拟)如图,在平面直角坐标系中,直线L:y=x是第一、三象限的角平分线. ,其中
,其中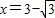 .
.