题目内容
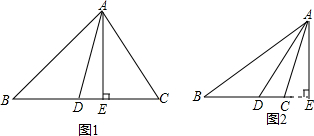
△ABC中，AD，BE分别是边BC，AC上的高，若∠EBC=∠BAD，则△ABC一定是
- A.等腰三角形
- B.等边三角形
- C.直角三角形
- D.等腰直角三角形
A
分析：发现∠ABC与∠C分别是∠BAD与∠EBC的余角，得到二角相等，根据等腰三角形的判定可得答案．
解答：
解：∵∠EBC+∠C=90°，∠C+∠CAD=90°，
∴∠CAD=∠EBC，
∵∠EBC=∠BAD
∴∠BAD=∠CAD，∠CAD+∠C=90°∠BAD+∠ABC=90°
∴∠ABC=∠C
∴AB=AC
∴为等腰三角形．
故选A．
点评：本题考查了等腰三角形的判定；由∠EBC=∠BAD利用等角的余角相等得到∠ABC=∠ACB是正确解答本题的关键．
分析：发现∠ABC与∠C分别是∠BAD与∠EBC的余角，得到二角相等，根据等腰三角形的判定可得答案．
解答：
解：∵∠EBC+∠C=90°，∠C+∠CAD=90°，∴∠CAD=∠EBC，
∵∠EBC=∠BAD
∴∠BAD=∠CAD，∠CAD+∠C=90°∠BAD+∠ABC=90°
∴∠ABC=∠C
∴AB=AC
∴为等腰三角形．
故选A．
点评：本题考查了等腰三角形的判定；由∠EBC=∠BAD利用等角的余角相等得到∠ABC=∠ACB是正确解答本题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
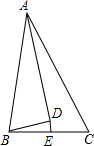已知：如图，△ABC中，AD平分∠BAC，BD⊥AD于D，点E是BC边的中点，AB=8，AC=12，求DE的长．
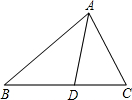如图，在△ABC中，AD平分∠BAC，AB=6，AC=4，△ABD的面积等于9．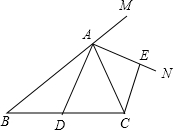
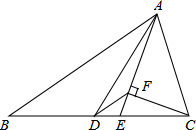（2013•乌鲁木齐）如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=5，AC=2，则DF的长为