题目内容
(2003•海淀区)已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连接DE.(1)如图,求证:DE是⊙O的切线;
(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAE的值.
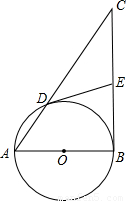
【答案】分析:(1)只要证∠EDO=90°,即可得到DE是⊙O的切线;
(2)根据平行的性质可得知:∠CAB=45°所以,sin∠CAE=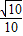 .
.
解答: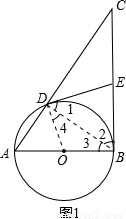 (1)证明:
(1)证明:
证法一:如图1,连接OD、DB;
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC边上的中点,
∴CE=EB=DE,
∴∠1=∠2.
∵OB=OD,
∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠ABC=∠2+∠3=90°,
∴∠EDO=∠1+∠4=90°.
∵D为⊙O上的点,
∴DE是⊙O的切线.
证法二:如图2,连接OD、OE.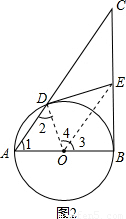
∵OA=OD,
∴∠1=∠2.
∵E为BC边上的中点,O为AB边上的中点,
∴OE∥AC,
∴∠1=∠3,∠2=∠4,
∴∠3=∠4.
∵OD=OB,OE=OE,
∴△EDO≌△EBO,
∴∠EDO=∠EBO.
∵△ABC为直角三角形,
∴∠EBO=90°,
∴∠EDO=90°;
∵D为⊙O上的点,
∴DE是⊙O的切线.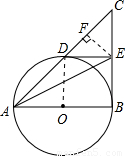
(2)解:∵∠CAB=45°时,D为线段AC的中点,切线DE∥AB,
四边形ODEB为正方形,此时,四边形AOED是平行四边形,
设AO=OB=2,则BE=EC=2,在Rt△ABE中,AE=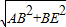 =
=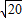 ,
,
易证△CEF为等腰直角三角形,则EF=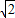 ,
,
∴sin∠CAE=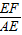 =
=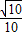 .
.
点评:主要考查了切线的判定方法和平行四边形的判定及其性质的运用.要掌握这些基本性质才会在综合习题中灵活运用.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.
(2)根据平行的性质可得知:∠CAB=45°所以,sin∠CAE=
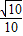 .
.解答:
 (1)证明:
(1)证明:证法一:如图1,连接OD、DB;
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC边上的中点,
∴CE=EB=DE,
∴∠1=∠2.
∵OB=OD,
∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠ABC=∠2+∠3=90°,
∴∠EDO=∠1+∠4=90°.
∵D为⊙O上的点,
∴DE是⊙O的切线.
证法二:如图2,连接OD、OE.

∵OA=OD,
∴∠1=∠2.
∵E为BC边上的中点,O为AB边上的中点,
∴OE∥AC,
∴∠1=∠3,∠2=∠4,
∴∠3=∠4.
∵OD=OB,OE=OE,
∴△EDO≌△EBO,
∴∠EDO=∠EBO.
∵△ABC为直角三角形,
∴∠EBO=90°,
∴∠EDO=90°;
∵D为⊙O上的点,
∴DE是⊙O的切线.

(2)解:∵∠CAB=45°时,D为线段AC的中点,切线DE∥AB,
四边形ODEB为正方形,此时,四边形AOED是平行四边形,
设AO=OB=2,则BE=EC=2,在Rt△ABE中,AE=
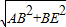 =
=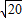 ,
,易证△CEF为等腰直角三角形,则EF=
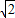 ,
,∴sin∠CAE=
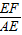 =
=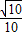 .
.点评:主要考查了切线的判定方法和平行四边形的判定及其性质的运用.要掌握这些基本性质才会在综合习题中灵活运用.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
(2003•海淀区)某同学在测量体温时意识到体温计的读数与水银柱的长度之间可能存在着某种函数关系,就此他与同学们选择了一种类型的体温计,经历了收集数据、分析数据、得出结论的探索过程,他们收集到的数据如下:
请你根据上述数据分析判断,水银柱的长度l(mm)与体温计的读数t(℃)(35≤t≤42)之间存在的函数关系是( )
A.
B.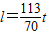
C.
D.
| 体温计的读数t(℃) | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 水银柱的长度l(mm) | 56.5 | 62.5 | 68.5 | 74.5 | 80.5 | 86.5 | 92.5 | 98.5 |
A.

B.
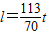
C.

D.


 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

 ,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.
,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边. ,若△ABC的周长为10,求抛物线的解析式;
,若△ABC的周长为10,求抛物线的解析式; 交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.